Zur Geschichte:
Schon in der Antike war einigen Mathematikern bekannt, dass es Zahlen gibt, die nicht als Bruch darstellbar sind. Sie zeigten das mit einem sogenannten indirekten Beweis:
Wäre z.B. die Diagonale eines Quadrats mit Seitenlängen 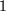 eine rationale Zahl, also
eine rationale Zahl, also 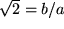 , dann gäbe es zwei natürliche Zahlen
, dann gäbe es zwei natürliche Zahlen  mit
mit 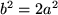 . Denken wir uns nun
. Denken wir uns nun 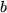 und
und  in ihre Primfaktoren zerlegt, so steht auf der linken Seite eine gerade Anzahl dieser Faktoren, wegen des Quadrats tritt jeder Faktor nämlich doppelt auf. Auf der rechten Seite hingegen steht eine ungerade Anzahl, denn es kommt ja noch der Faktor 2 hinzu. Da die Zerlegung in Primfaktoren eindeutig ist, kann die Gleichung also nicht richtig sein.
in ihre Primfaktoren zerlegt, so steht auf der linken Seite eine gerade Anzahl dieser Faktoren, wegen des Quadrats tritt jeder Faktor nämlich doppelt auf. Auf der rechten Seite hingegen steht eine ungerade Anzahl, denn es kommt ja noch der Faktor 2 hinzu. Da die Zerlegung in Primfaktoren eindeutig ist, kann die Gleichung also nicht richtig sein.
Damit ist gezeigt, dass die Annahme, 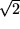 könne als Bruch dargestellt werden, zu einem Widerspruch führt, also falsch sein muß.
könne als Bruch dargestellt werden, zu einem Widerspruch führt, also falsch sein muß.
Zurück zum Text
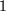 eine rationale Zahl, also
eine rationale Zahl, also 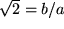 , dann gäbe es zwei natürliche Zahlen
, dann gäbe es zwei natürliche Zahlen  mit
mit 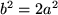 . Denken wir uns nun
. Denken wir uns nun 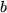 und
und  in ihre Primfaktoren zerlegt, so steht auf der linken Seite eine gerade Anzahl dieser Faktoren, wegen des Quadrats tritt jeder Faktor nämlich doppelt auf. Auf der rechten Seite hingegen steht eine ungerade Anzahl, denn es kommt ja noch der Faktor 2 hinzu. Da die Zerlegung in Primfaktoren eindeutig ist, kann die Gleichung also nicht richtig sein.
in ihre Primfaktoren zerlegt, so steht auf der linken Seite eine gerade Anzahl dieser Faktoren, wegen des Quadrats tritt jeder Faktor nämlich doppelt auf. Auf der rechten Seite hingegen steht eine ungerade Anzahl, denn es kommt ja noch der Faktor 2 hinzu. Da die Zerlegung in Primfaktoren eindeutig ist, kann die Gleichung also nicht richtig sein.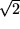 könne als Bruch dargestellt werden, zu einem Widerspruch führt, also falsch sein muß.
könne als Bruch dargestellt werden, zu einem Widerspruch führt, also falsch sein muß.