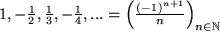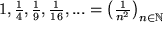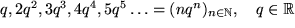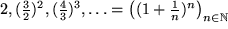Der erste wichtige mathematische Begriff, mit dem wir uns beschäftigen müssen, ist der einer Folge.
Der Physiker denkt dabei etwa an die Folge der Sprunghöhen einer Stahlkugel auf einer Platte, die infolge der unvermeidlichen Energiedissipation mit der Zeit monoton abnehmen und schließlich mehr oder weniger schnell gegen Null streben. Nach einiger Zeit bleibt die Kugel ruhig liegen. Die physikalische Folge der Sprunghöhen hat also nur endlich viele nicht verschwindende Glieder im Gegensatz zu den Folgen, die in der Mathematik interessieren:
Mathematisch ist eine Folge eine unendliche Menge von Zahlen, die durchnumeriert, d.h. auf die Menge der natürlichen Zahlen abgebildet werden kann: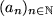 
. Da man nicht alle unendlich vielen Glieder angeben kann 
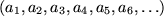, definiert man eine Folge meist durch das "allgemeine Glied" 
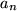, d.h. das Bildungsgesetz, das angibt, wie man die Glieder berechnet. Wir wählen zunächst einige charakteristische Musterbeispiele aus, an denen wir aber bereits alles Wichtige erklären können:
| (F1) |  |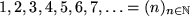
die natürlichen Zahlen selbst, |
| (F2) |  |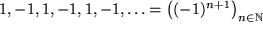
eine einfache "alternierende" Folge, |
| (F3) |  |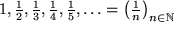
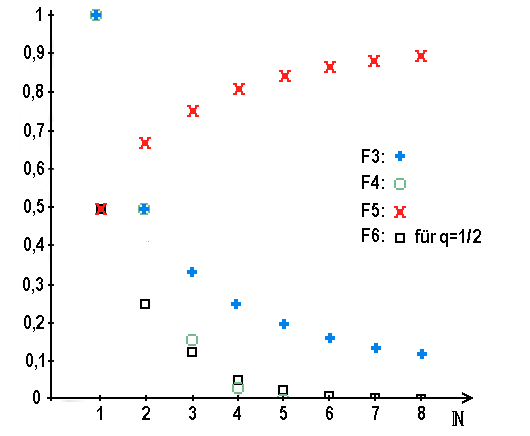
die inversen natürlichen Zahlen, die sogenannte "harmonische" Folge, |
| (F4) |  |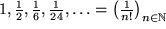
die inversen Fakultäten, |
| (F5) |  |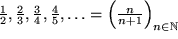
eine Folge von echten Brüchen und |
| (F6) |  ,  |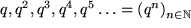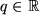
die "geometrische" Folge. |
Um uns eine erste anschauliche Vorstellung von diesen Musterfolgen zu geben, sind im ebenen kartesischen Koordinatensystem der folgenden graphischen Darstellungen die Folgenglieder (in 2-Richtung) über den äquidistanten natürlichen Zahlen 
(in 1-Richtung) durch Punkte eingetragen:
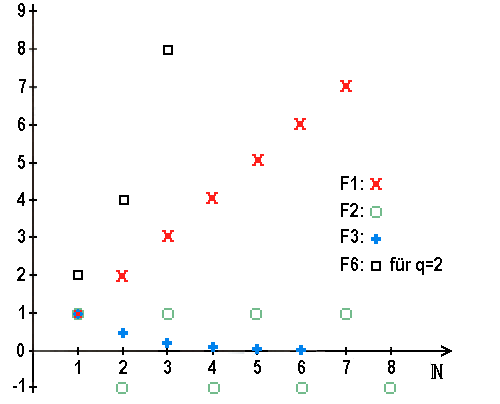
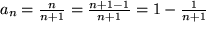die Differenz aus der trivialen Folge 
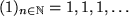, die aus lauter Einsen besteht, und der harmonischen Folge (F3) bis auf das erste Glied.
