An der Folge F3: 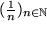wollen wir alle Konvergenzkriterien ausprobieren:

(1) Am leichtesten prüft man den Satz von Bolzano und Weierstraß: Die Folge (F3) 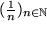fällt monoton und ist nach unten beschränkt: 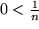, also konvergiert sie.

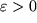(2) Der Häufungspunkt liegt offensichtlich bei : Wir geben ein willkürlich vor, z.B. 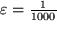und suchen die Nummer 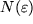, so dass 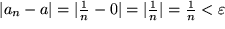für .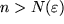
Das ist aber sicher der Fall, wenn wir 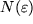als die nächst größere natürliche Zahl größer als wählen: 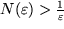(z.B. bei 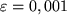also 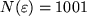. Dann gilt für alle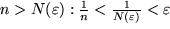

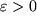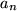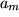(3) Endlich ist auch das Cauchy-Kriterium hier leicht nachzurechnen: Sei ein vorgegeben, so folgt für den Abstand zweier Glieder und mit 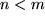: 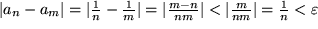, falls .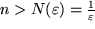