:Folge gegen :
Neben dieser Exponential-Reihe, die wir zur Definition von verwendet haben, gibt es wie anfangs erwähnt noch eine Folge, die gegen die Zahl konvergiert, die Exponential-Folge (F10): 
,..., der wir uns zum Vergleich noch kurz zuwenden wollen:
Nach der binomischen Formel erhalten wir zunächst für das allgemeine Glied:
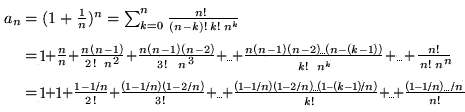
Einerseits vergrößern wir nun diesen Ausdruck für 
, indem wir in den Klammern keine Vielfachen von 
mehr abziehen:
und erhalten so bis auf die Eins die entsprechende Teilsumme der Exponential-Reihe 
. Damit ist die Exponential-Reihe eine Majorante für die ebenfalls monoton steigende Exponential-Folge und deren Konvergenz durch die der Reihe gesichert: Für den Grenzwert erhalten wir:
Andererseits verkleinern wir den obigen Ausdruck für , indem wir von den durchweg positiven Summanden nur 
Stück mitnehmen und die letzten weglassen:
Wenn wir jetzt zunächst die größere der natürlichen Zahlen, 
, über alle Grenzen wachsen lassen, erhalten wir:
und nachdem auch die kleinere natürliche Zahl: 
über alle Grenzen gewachsen ist:
Folglich muß der Grenzwert 
der Exponential-Folge gleich der durch die Exponential-Reihe definierten Zahl sein:
Wenn Sie sich allerdings die Glieder der Folge ausrechnen und mit den Teilsummen der Reihe ergleichen, werden Sie feststellen, dass die Folge viel langsamer konvergiert als die Reihe.