4 Funktionen
4.1 Funktion als Input-Output-Relation oder Abbildung
Die Physiker denken dabei z.B. an einen elektrischen Stromkreis, bei dem die angelegte Spannung an einem Potentiometer schrittweise verändert und mit einem Drehspulgalvanometer die jeweilige Stromstärke gemessen wird, um die Kennlinie zu erforschen. Aber auch der zeitliche Verlauf des Ausschlags eines Pendels oder die radioaktiv zerfallende Stoffmenge als Funktion der Zerfallszeit sind weitere aus der Vielzahl von physikalischen Beispielen.
Das Resultat einer solchen Messreihe ist zunächst eine Wertetabelle  . Die Daten können auch in einer graphischen Darstellung veranschaulicht werden, wie unten im Bild an Beispielen gezeigt. Die Veranschaulichung der Funktionen als Schaubild, von uns meist Graph genannt, durch Eintragen der Wertetabelle in ein ebenes kartesisches ( d.h. rechtwinkliges ) Koordinatensystem mit der Abszisse
. Die Daten können auch in einer graphischen Darstellung veranschaulicht werden, wie unten im Bild an Beispielen gezeigt. Die Veranschaulichung der Funktionen als Schaubild, von uns meist Graph genannt, durch Eintragen der Wertetabelle in ein ebenes kartesisches ( d.h. rechtwinkliges ) Koordinatensystem mit der Abszisse  auf der 1-Achse und der Ordinate
auf der 1-Achse und der Ordinate 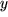 auf der 2-Achse ist für die Physiker selbstverständlich.
auf der 2-Achse ist für die Physiker selbstverständlich.
Bilder 4.2: In den folgenden Abbildungen finden Sie Beispiele für
Wertetabellen, graphische Darstellungen und interpolierende Funktionen
für eine schwindende Spiralfeder
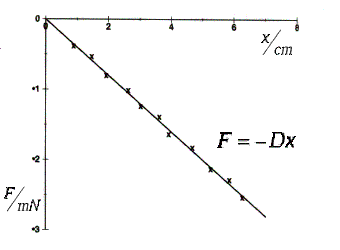
1) Rücktreibende Kraft
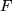
der Feder gemessen in mN in Abhängigkeit von der Auslenkung

in cm,
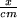 |
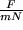 |
| 1 |
-0,42 |
| 1,5 |
-0,55 |
| 2 |
-0,82 |
| 2,5 |
-1,03 |
| 3 |
-1,25 |
| 3,5 |
-1,45 |
| 4 |
-1,65 |
| 4,5 |
-1,80 |
| 5 |
-1,95 |
| 5,5 |
-2,20 |
| 6 |
-2,35 |
| 6,6 |
-2,60 |
|
|
 |
2) In der Feder gespeicherte potentielle Energie 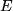 gemssen in mJ in Abhängigkeit von der Auslenkung
gemssen in mJ in Abhängigkeit von der Auslenkung  in cm,
in cm,
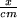 |
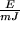 |
| 1 |
0,6 |
| 1,5 |
1,0 |
| 2,5 |
2,8 |
| 2,9 |
3,9 |
| 3,1 |
4,8 |
| 3,5 |
6,1 |
|
|
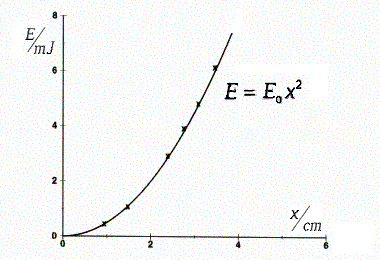 |
3) Auslenkung der Spiralfeder  gemesse in cm in Abhängigkeit von der Zeit
gemesse in cm in Abhängigkeit von der Zeit 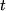 in
in  ,
,
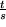 |
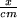 |
| 0,3 |
3,5 |
| 0,5 |
2,8 |
| 0,7 |
1,2 |
| 1,1 |
-1,8 |
| 1,4 |
-3,2 |
| 1,7 |
-3,1 |
| 2,4 |
-0,8 |
| 2,6 |
1,5 |
| 3,2 |
2,4 |
| 3,6 |
1,4 |
| 4,3 |
-1,1 |
| 4,8 |
-1,8 |
|
|
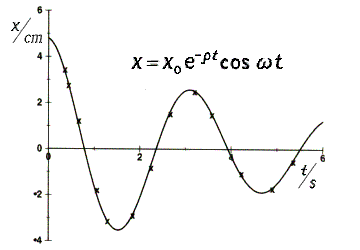 |
4) Schwingungsdauer der Spiralfeder 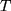 in
in  als Funktion der Masse
als Funktion der Masse
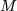 in g bei unveränderter
Federkonstante
in g bei unveränderter
Federkonstante 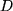 ,
,
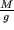 |
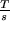 |
| 2,5 |
0,75 |
| 10 |
1,63 |
| 14 |
1,91 |
| 20 |
2,23 |
| 25 |
2,46 |
|
|
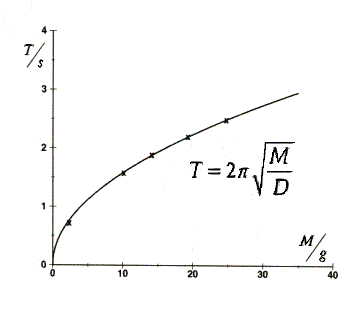 |
5) Schwingungsdauer 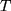 der
Spiralfeder in
der
Spiralfeder in  als Funktion der
Richtkraft
als Funktion der
Richtkraft 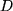 gemessen in
gemessen in
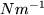 bei unveränderter Masse
bei unveränderter Masse
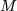 .
.
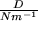 |
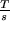 |
| 3 |
3,253 |
| 4 |
2,72 |
| 5 |
2,16 |
| 7 |
1,75 |
| 8 |
1,71 |
| 10 |
1,59 |
|
|
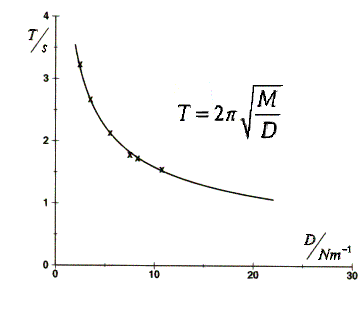 |
Wenn man sich über die unvermeidlichen Meßfehler Rechenschaft gegeben hat, kann man daran gehen, die Meßwerte durch eine Kurve zu verbinden bzw. eine mathematische Rechenvorschrift, d.h. Funktion zu suchen, die die Abhängigkeit der beiden Größen beschreibt. Gelingt es, eine solche Funktion zu finden, hat das viele Vorteile: Eine mathematische Formel ist meist kurz und übersichtlich; sie kann viel leichter als umfangreiche Wertetabellen gestapelt, weiterverarbeitet und anderen Interessenten mitgeteilt werden. Mit ihrer Hilfe kann auch genauer zwischen den Meßwerten interpoliert und über den untersuchten Bereich hinaus extrapoliert werden, was wieder neue Experimente anregt. Endlich ist sie der erste Schritt zu einer Theorie und damit zum Verständnis des Experiments.
Wir müssen uns also aus physikalischen Gründen mit Funktionen befassen, und zwar zunächst mit reellen Funktionen einer reellen Variablen.
Mathematisch kann eine Funktion 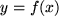 betrachtet werden als eindeutige Abbildung
betrachtet werden als eindeutige Abbildung 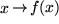 eines Punktes aus einem Bereichs
eines Punktes aus einem Bereichs 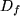 , dem "Definitionsbereichs" von
, dem "Definitionsbereichs" von 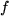 , der unabhängigen Variablen
, der unabhängigen Variablen  ( auch Abszisse oder Argument genannt ) auf einen Punkt
( auch Abszisse oder Argument genannt ) auf einen Punkt  aus dem Bereich
aus dem Bereich 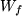 , dem "Wertevorrat" von
, dem "Wertevorrat" von 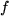 , der abhängigen Variablen
, der abhängigen Variablen 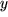 ( auch Ordinate oder Funktionswert genannt ).
( auch Ordinate oder Funktionswert genannt ).
Während die Angabe des Definitionsbereichs neben der Abbildungsvorschrift für eine Funktion unbedingt erforderlich ist und oft über die Eigenschaften der Funktion entscheidet, ist die genaue Angabe des Wertevorrats 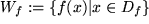 meist von geringerer Wichtigkeit und erfordert manchmal einige Mühe.
meist von geringerer Wichtigkeit und erfordert manchmal einige Mühe.
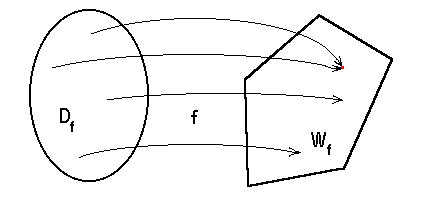
Bild 4.3: Funktion f als Abbildung des Definitionsbereichs Df in den Wertevorrat Wf mit zwei Pfeilen, die von zwei Urbildpunkten zu einem Bildpunkt führen.
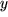 als Funktion von
als Funktion von  " oder
" oder 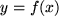 : Dabei wird die eine Größe
: Dabei wird die eine Größe  , unabhängige Variable genannt, messbar verändert und die zweite Größe
, unabhängige Variable genannt, messbar verändert und die zweite Größe 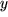 , die abhängige Variable, jeweils gemessen. Man mag sich die Messapparatur wie im beigefügten Bild als schwarzen Kasten vorstellen, in den die
, die abhängige Variable, jeweils gemessen. Man mag sich die Messapparatur wie im beigefügten Bild als schwarzen Kasten vorstellen, in den die  als Input eingegeben werden und aus dem die zugehörigen
als Input eingegeben werden und aus dem die zugehörigen 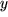 als Output herauskommen.
als Output herauskommen.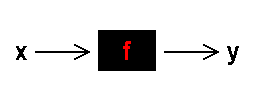
 . Die Daten können auch in einer graphischen Darstellung veranschaulicht werden, wie unten im Bild an Beispielen gezeigt. Die Veranschaulichung der Funktionen als Schaubild, von uns meist Graph genannt, durch Eintragen der Wertetabelle in ein ebenes kartesisches ( d.h. rechtwinkliges ) Koordinatensystem mit der Abszisse
. Die Daten können auch in einer graphischen Darstellung veranschaulicht werden, wie unten im Bild an Beispielen gezeigt. Die Veranschaulichung der Funktionen als Schaubild, von uns meist Graph genannt, durch Eintragen der Wertetabelle in ein ebenes kartesisches ( d.h. rechtwinkliges ) Koordinatensystem mit der Abszisse 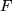 der Feder gemessen in mN in Abhängigkeit von der Auslenkung
der Feder gemessen in mN in Abhängigkeit von der Auslenkung 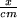
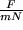

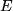 gemssen in mJ in Abhängigkeit von der Auslenkung
gemssen in mJ in Abhängigkeit von der Auslenkung 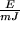
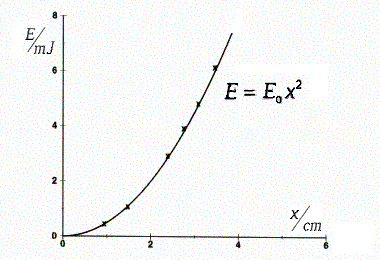
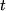 in
in  ,
,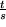
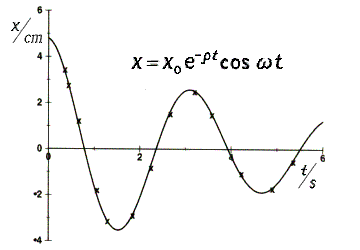
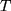 in
in 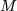 in g bei unveränderter
Federkonstante
in g bei unveränderter
Federkonstante 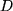 ,
,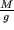
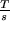
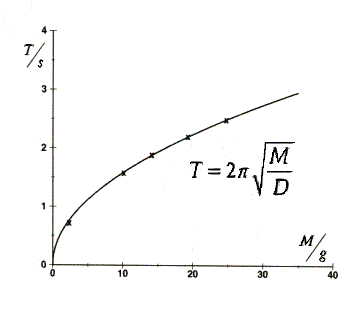
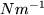 bei unveränderter Masse
bei unveränderter Masse
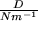
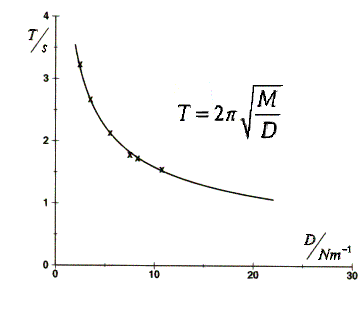
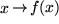 eines Punktes aus einem Bereichs
eines Punktes aus einem Bereichs 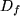 , dem "Definitionsbereichs" von
, dem "Definitionsbereichs" von 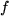 , der unabhängigen Variablen
, der unabhängigen Variablen  aus dem Bereich
aus dem Bereich 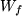 , dem "Wertevorrat" von
, dem "Wertevorrat" von 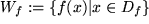 meist von geringerer Wichtigkeit und erfordert manchmal einige Mühe.
meist von geringerer Wichtigkeit und erfordert manchmal einige Mühe.
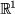 . Die ausdrücklich in die Definition der reellen Funktionen mit einbezogene Eindeutigkeit bedeutet, dass es zu jedem
. Die ausdrücklich in die Definition der reellen Funktionen mit einbezogene Eindeutigkeit bedeutet, dass es zu jedem 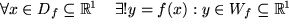
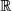 mit den beiden Kommutativen und Assoziativen Gesetzen sowie dem verbindenden Distributivgesetz, die wir im
mit den beiden Kommutativen und Assoziativen Gesetzen sowie dem verbindenden Distributivgesetz, die wir im 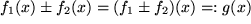 eine neue reelle Funktion, das reelle Vielfache
eine neue reelle Funktion, das reelle Vielfache 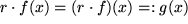 mit
mit  ebenfalls und analog das Produkt
ebenfalls und analog das Produkt 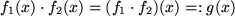 oder, falls
oder, falls 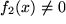 im gesamten Definitionsbereich, auch der Quotient
im gesamten Definitionsbereich, auch der Quotient 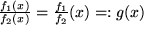 .
.