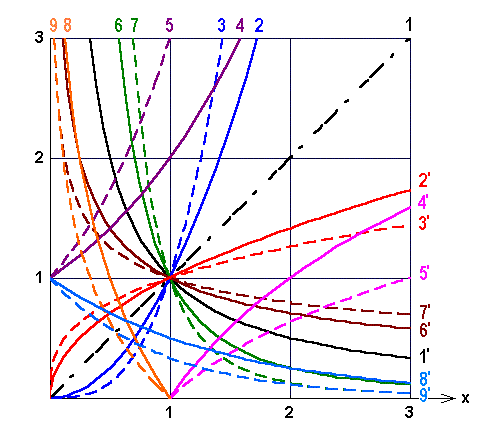
Bild 4.28: Funktionen-Quiz
Lösung:

Bild 4.28: Funktionen-Quiz
Man erkennt sogleich
| 1) | die Winkelhalbierende |
| 2) | die Normal-Parabel |
| 3) | die kubische Parabel |
| 2') | die Quadratwurzel |
| 3') | die Kubikwurzel |
Dann sieht man ebenfalls durch den Punkt (1,1) laufend
| 1') | die schwarz durchgezogene Einheitshyperbel |
| 6) | |
| 7) |
Als deren Umkehrfunktionen erkennt man in Braun flacher abfallend
| 6') | |
| 7') |
Damit sind alle durch (1,1) laufenden Graphen identifiziert.
Welche einfachen Graphen laufen nun typischerweise durch den Punkt (0,1)?
Richtig, die Exponentialfunktionen: zunächst identifiziert man monoton wachsend in Violett:
| 4) | durch den Punkt (1,2) wegen |
| 5) | durch (1,3) als |
Als deren Umkehrfunktionen erhält man daraus in Magenta:
| 4') | |
| 5') |
Schließlich bleiben nur noch die beiden abfallenden Exponentialfunktionen in Hellblau:
| 8') | |
| 9') | |
| 8) | |
| 9) |