4 Funktionen

4.2 Funktionen-Grundausstattung

4.2.1 Rationale Funktionen

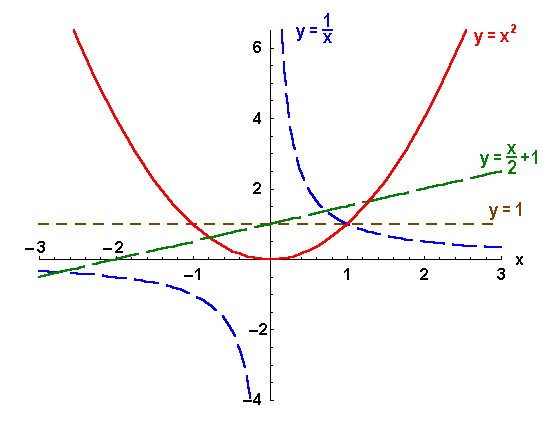
Wir beginnen mit der konstanten Funktion , unabhängig von . Danach kommen wir zu den linearen Funktionen mit dem Graph einer Geraden der Steigung und dem Ordinatenabschnitt . Es folgt die Normal-Parabel und die höheren Potenzen mit . Auch die Normal-Hyperbel und sind Ihnen sicher schon begegnet.

Gerade und Parabel sind z.B. über der ganzen reellen Gerade definiert: . Bei der Hyperbel muß der Nullpunkt ausgenommen werden: . Auch beim Wertevorrat der Hyperbel fehlt der Nullpunkt: . Bei der Parabel ist der Wertevorrat nur die positive Halbgerade einschließlich der Null: . Das folgende Bild zeigt die Graphen dieser einfachen Beispiele:

Bild 4.4: Graphen einfacher Funktionen

Nach den Rechenregeln des Körpers der reellen Zahlen erhalten wir aus der Geraden und der Normal-Parabel alle Funktionen zweiten Grades sowie weiter alle Polynomfunktionen höheren, z.B. -ten Grades

Auch die allgemeine rationale Funktion

mit einem Polynom -ten Grades im Zähler und einem Polynom -ten Grades im Nenner sind Ihnen schon begegnet, z.B. , die Lorentz-Verteilung, die unter anderem die Linienbreite einer Spektrallinie beschreibt, mit und oder . Diese rationalen Funktionen sind für alle definiert außer für solche Werte , für die der Nenner verschwindet: .