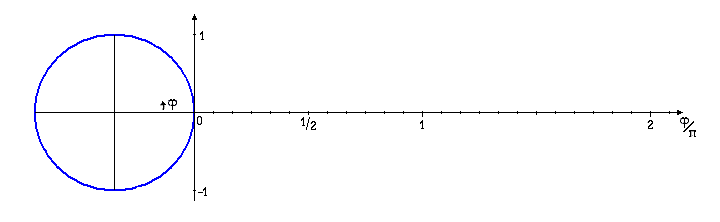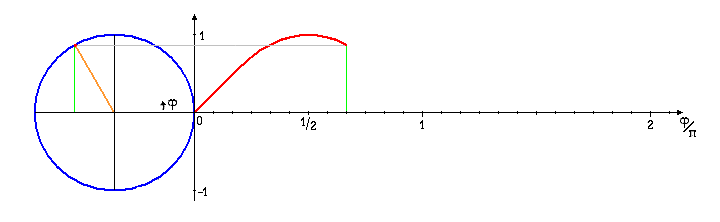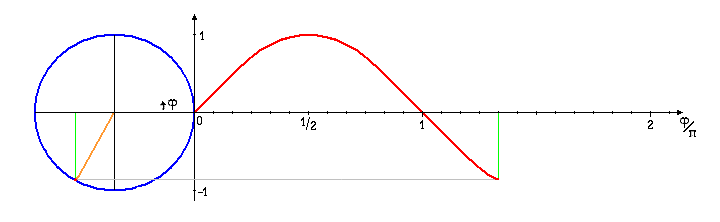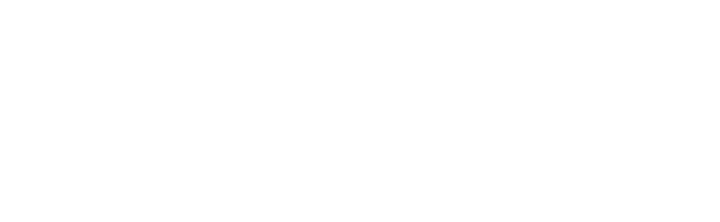
Bild 4.5: Aufbau der Sinus-Funktion: Drehbar gedachte Kreisscheibe mit Tintenpatrone auf dem Umfang,
unter der eine Zeichnung des Graph
von ![]() herausgezogen werden kann.
herausgezogen werden kann.
Eine weitere Gruppe von fundamentalen Funktionen aller Naturwissenschaften kennen Sie ebenfalls von der Schule: die trigonometrischen Funktionen. Sie spielen bei allen periodischen Prozessen, sei es im Raum oder in der Zeit, eine zentrale Rolle, z.B. bei der Bewegung eines Pendels, bei der Beschreibung von Licht- und Schallwellen und auch bei den Schwingungen einer Saite.
Klicken Sie im folgenden Bild auf die um ihren Mittelpunkt drehbare Einheitskreisscheibe mit einer gedachten Tintenpatrone auf ihrem Rand am Ende des roten Radius und ziehen Sie mit der Maus das unterliegende graue Papierblatt nach rechts unter der sich gleichförmig drehenden Scheibe heraus und betrachten Sie die Kurve, die Ihnen die Patrone auf das Papier gemalt hat:
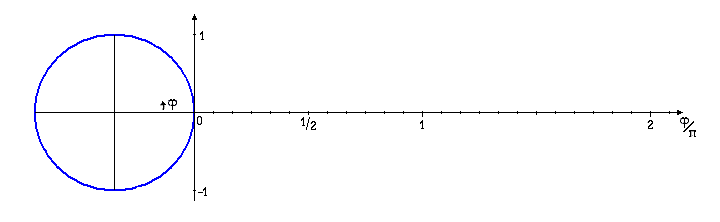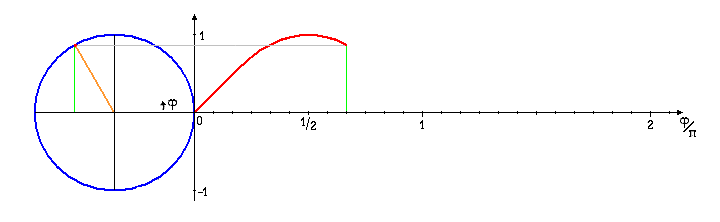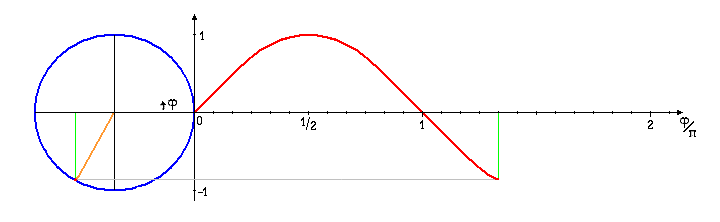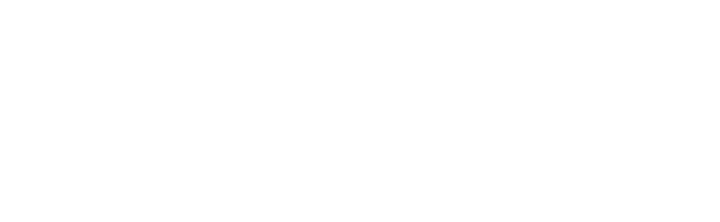
Bild 4.5: Aufbau der Sinus-Funktion: Drehbar gedachte Kreisscheibe mit Tintenpatrone auf dem Umfang,
unter der eine Zeichnung des Graph
von ![]() herausgezogen werden kann.
herausgezogen werden kann.
Die Patrone hat uns dabei mit der Projektion des umlaufenden Zeigers auf die 2-Achse die "Länge der Gegenkathete" in dem vom umlaufenden Radius der Länge ![]() als Hypotenuse gebildeten rechtwinkligen Dreieck, also den Graph der Funktion
als Hypotenuse gebildeten rechtwinkligen Dreieck, also den Graph der Funktion ![]() , den "Sinus" als Funktion des Winkels aufs Blatt gemalt.
, den "Sinus" als Funktion des Winkels aufs Blatt gemalt.
Offensichtlich ergibt diese Konstruktionsvorschrift eine periodische Funktion, d.h. in Abständen der unabhängigen Variablen von ![]() nimmt die abhängige Variable die gleichen Werte an:
nimmt die abhängige Variable die gleichen Werte an: ![]() , allgemein:
, allgemein:
Aus der Sinus-Funktion kann man durch einfache Operationen andere trigonometrische Funktionen bilden, die wegen ihrer Wichtigkeit eigene Namen bekommen haben:
Die "Cosinus-Funktion" ![]() erhalten wir analog wie die Sinus-Funktion als "Länge der Ankathete" des Winkels
erhalten wir analog wie die Sinus-Funktion als "Länge der Ankathete" des Winkels ![]() in dem vom rotierenden Radius und dem Sinus gebildeten rechtwinkligen Dreieck oder als Projektion des umlaufenden Zeigers jetzt auf die 1-Achse. Der fundamentale Zusammenhang
in dem vom rotierenden Radius und dem Sinus gebildeten rechtwinkligen Dreieck oder als Projektion des umlaufenden Zeigers jetzt auf die 1-Achse. Der fundamentale Zusammenhang
folgt mit dem Satz des Pythagoras unmittelbar aus dem im Bild markierten Dreieck. Die Tintenpatrone hätte uns offensichtlich sofort den Cosinus gemalt, wenn wir mit dem Winkel ![]() statt
statt ![]() begonnen hätten:
begonnen hätten:
Die Cosinusfunktion ist also eine um die "Phase" ![]() nach links verschobene Sinusfunktion.
nach links verschobene Sinusfunktion.
Auch der Cosinus ist periodisch mit der Periode ![]() :
: ![]() .
.
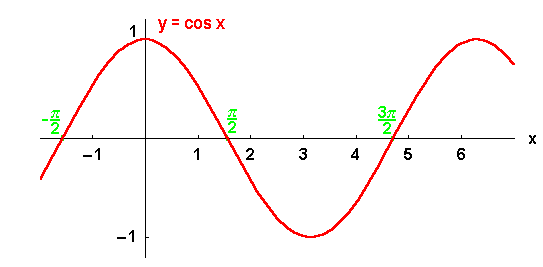
Bild 4.6: Graph des Cosinus
Aus Sinus und Cosinus erhält man durch Division zwei weitere wichtige trigonometrische Funktionen: den
und den
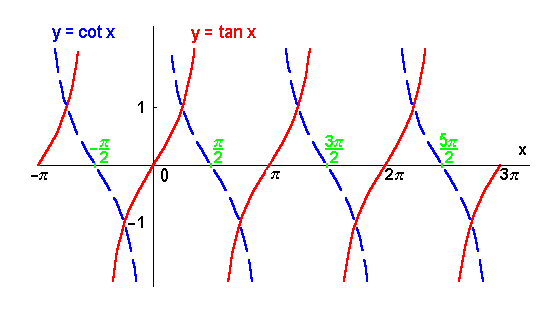
Bild 4.7: Tangens und Cotangens
Tangens und Cotangens sind periodisch mit der Periode ![]() :
: ![]() .
.
Wir werden im Kapitel 6 lernen, wie man den Funktionswert auch der trigonometrischen Funktionen z.B. von ![]() zu jedem Wert der Variablen
zu jedem Wert der Variablen ![]() durch elementare Rechenoperationen wie Addition und Multiplikation berechnen kann.
durch elementare Rechenoperationen wie Addition und Multiplikation berechnen kann.
Ganz wichtig sind neben der Pythagoras-Relation ![]() die:
die:
Trigonometrischen Additionstheoreme :
![]()
![]()
die wir Ihnen erfahrungsgemäß in Erinnerung rufen müssen und zum Auswendiglernen empfehlen. Wir werden sie im Kapitel 8 auf sehr viel elegantere Weise als in der Schule herleiten.
|
Aufgabe 4.2: Trigonometrische Funktionen Skizzieren Sie die Graphen und Definitionsbereiche von folgenden Funktionen und außer beim letzten Beispiel auch die Wertevorräte:
Ihre Skizzen kontrollieren Sie mit dem Funktionenschaufenster oder z.B. graph.tk oder www.wolframalpha.com. |