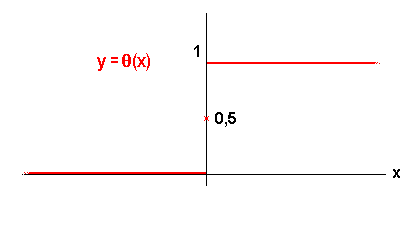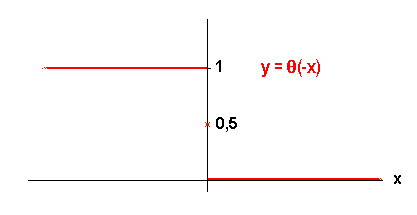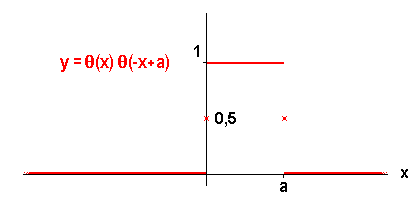Außer diesen Beispielfunktionen benützen die Physiker häufig noch einige Funktionen, deren Graphen Ecken ( oder Knicke ) bzw. Sprünge ( oder Treppen ) aufweisen. Unter diesen sind uns zwei besonders wichtig:
Die eine ist die
Betragsfunktion: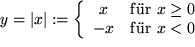 
Sie ist über der ganzen Zahlengeraden definiert, wie bei der Normalparabel umfaßt ihr Wertebereich aber nur die nicht negative Halbgerade: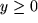 
. Das nächste Bild zeigt ihren Graph mit der "Ecke" bei 
.
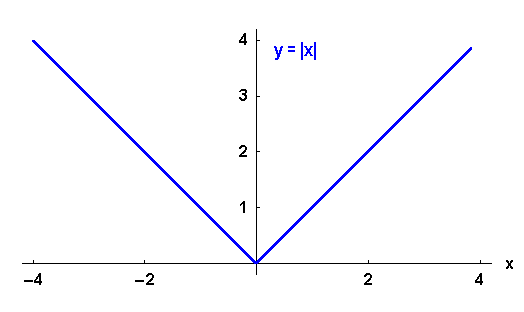
Bild 4.12: Graph der Betragsfunktion
|
Aufgabe 4.4: Betragsfunktionen Skizzieren Sie die Graphen und Wertevorräte folgender Funktionen: a) b) c) d) Bei der Kontrolle Ihrer Skizzen kann das Funktionenschaufenster helfen. |
Die andere ist eine Funktion, die Ihnen vermutlich bisher noch nicht begegnet ist: die Heavisidesche Stufenfunktion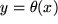 
, definiert durch
Heavisidesche Stufenfunktion: 
für 
, 
für 
und 
.
Das Bild zeigt ihren Graph mit der charakteristischen zweiteiligen Stufe bei x = 0.
Bild 4.13: Heaviside-Funktion 
: "treppauf bei 
"
Man kann sich leicht vorstellen, dass die Heaviside-Funktion in der Physik unter anderem bei Ein- und Ausschaltvorgängen oder zur Beschreibung von Stufen und Schwellen gebraucht wird.
Das Rechnen mit der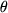 
-Funktion erfordert etwas Übung, die wir uns im folgenden verschaffen wollen:
Wir stellen zunächst fest, dass
falls das Argument mit einer positiven reellen Zahl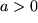 
multipliziert wird. Dann betrachten wir
Bild 4.14: Graph von 
: "treppab bei "
Um uns ein Bild von 
zu machen, überlegen wir, dass die Funktion verschwindet, wo das Argument 
, also 
ist, d.h. der Graph ist "treppauf bei 
". Analog bedeutet 
"treppauf bei 
" und 
"treppab bei ".
Interessant sind noch die Produkte von zwei Stufenfunktionen: z.B. 
. Bei gleichem Vorzeichen der Variablen setzt sich das kleinere Argument durch. Bei verschiedenen Vorzeichen der Variablen im Argument erhalten wir entweder identisch , wie bei 
oder eine Schwelle wie bei 
mit folgendem Graph: "treppauf bei und treppab bei ":
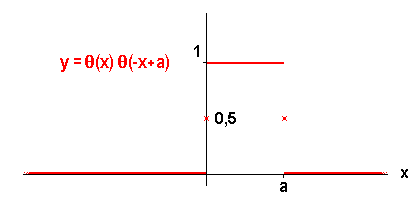
Bild 4.15: Graph des Produkts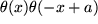 
|
Aufgabe 4.5: Heaviside Funktion: mit a>0
|
-