Neben den Möglichkeiten, die der Körper der reellen Zahlen mit Addition, Subtraktion, Multiplikation
und Division bietet, um aus den Funktionen unserer Grundausstattung neue Funktionen zu bilden, gibt es
dazu auch eine wichtige neue Operation, nämlich die Möglichkeit der verketteten oder mittelbaren Funktionen,
auch Schachtelfunktionen genannt. Sie besteht darin, dass man "eine Funktion in eine andere
Funktion einsetzt": Falls z.B. der Wertevorrat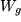 
einer ("inneren") Funktion 
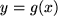im Definitionsbereich
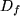einer
anderen ("äußeren") Funktion 
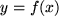liegt: 
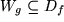, erhalten wir mit 
, wobei 
, eine neue funktionale Abhängigkeit, die manchmal auch mit
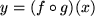bezeichnet wird. Da wir die Bezeichnungen für die unabhängige und abhängige Varable frei wählen können,
wird der Schachtelvorgang besonders klar, wenn wir schreiben: 
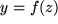mit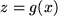 
) ergibt :
Einfache Beispiele sind etwa:
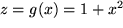mit
als innere Funktion und
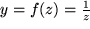mit
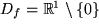als äußere, was die Lorentz-Verteilungsfunktion als Schachtelfunktion
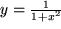ergibt,
oder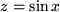 
mit
eingesetzt in
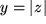mit
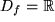ergibt
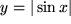zur Beschreibung von gleichgerichtetem Wechselstrom,
oder auch 
mit
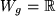eingesetzt in
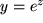ergibt
,
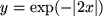eine exponentiellle Spitze.
Auch die Gaußsche Glockenkurve
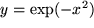, entstanden aus
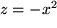mit
und
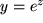ist eine interessante verkettete Funktion, die in allen Naturwissenschaften häufig gebraucht wird.
|
Aufgabe 4.6.: Verkettete Funktionen
Skizzieren Sie die Graphen der obigen Beispiele und untersuchen und skizzieren Sie folgende
Schachtel-Funktionen:
a)
 , |
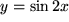b)
 , |
c)
 , |
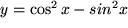d)
 , |
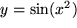e)
 , |
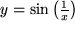f)
 ,
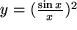die z.B. die Lichtintensität nach einer Beugung beschreibt, |
g)
 , |
h) die klassische Maxwell-Boltzmannsche Geschwindigkeitsverteilung für die
zusammenstoßenden Moleküle eines idealen Gases
 , |
i) die Bose-Einstein-Verteilung der Geschwindigkeiten eines Gases nach der
Quantenstatistik
 , |
j) die Fermi-Dirac-Verteilung für die Geschwindigkeiten im
Elektronengas
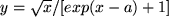mit der temperaturabhängigen Konstante
 , |
k) die Plancksche Strahlungsformel für die spektrale Intensitätsverteilung der
Wellenlängen eines Hohlraumstrahlers
 , |
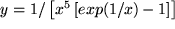l)
 , |
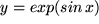m)
 , |
n)
 . |
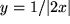| Ihre Skizzen kontrollieren Sie mit dem JAVA-Funktionenschaufenster
unten oder z.B. fooplot.com,
graph.tk oder auch www.wolframalpha.com. |
|
Dieses Fenster zeigt Ihnen in einem kartesichen Koodinatensystem die Graphen aller Funktionen, die Sie aus
unserer Funktionen-Grundausstattung als Linearkombinationen, Produkte oder Schachtelfunktionen aufbauen können:
Sie tippen in das Feld rechts oben die interessierende Funktion ein, indem Sie
als Symbol für die
unabhängige Variable verwenden und die Funktionen computergerecht schreiben (mit einer reellen Zahl
): Die Zahl
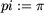kennt der Plotter, aber die Eulerzahl
ist ihm unbekannt.
Addition, Subtraktion und Division wie gewohnt:
,
Multiplikation mit einem Stern statt Punkt:
,
Potenzieren mit dem Dach:
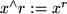und
,
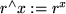Quadratwurzelziehen mit sqrt(x)
,
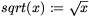sonstige Wurzeln müssen sie als gebrochene Exponenten eingeben,
trigonometrische Funktionen mit Klammern:
,
,
,
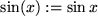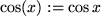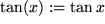Exponentialfunktion mit
, denn die Zahl
kennt der Plotter nicht,
Hyperbelfunktionen ebenfalls mit Klammern:
,
,
.
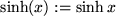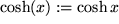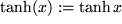Er kennt nur die drei gängigen Logarithmen:
,
und
.
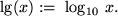Die Betragsfunktion und die Heaviside-Funktion können Sie sich selbst durch Intervallteilung synthetisieren.
Nur runde Klammern sind zugelassen.
Den Maßstab können Sie in den beiden Richtungen unabhängig innerhalb weiter Grenzen durch
Anklicken der Lupenzeichen verändern. Wenn Sie mit den Vorbereitungen fertig sind, starten Sie
die Zeichnung mit der Return-Taste.
Dieses von Thomas Fuhrmann programmierte einfache Funktionenschaufenster berechnet die gewünschten
Funktionen natürlich nur an wenigen Punkten und gibt deren Verlauf nur grob wieder.
Besonders in der Nähe von Singularitäten sind seine Bilder deshalb mit Vorsicht zu genießen.
Spielen Sie mit dem Funktionenschaufenster. Viel Vergnügen!
Wenn Sie am Ende Ihrer Wünsche und Fantasie angelangt sind, schlagen wir vor, den Aufbau von
interessanten Funktionen-Reihen zu studieren: z.B.
a) im Intervall [-0,99, 0,99]: zunächst
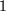, dann
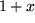, dann
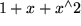, dazu
,
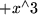, usw.
und immer vergleichen mit
,
b) im Intervall [-0,1, 0,1]:
usw.,
zu vergleichen mit
,
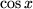c) im Intervall
:
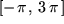Was kommt dabei heraus?
d) im Intervall
:
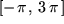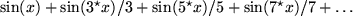
Wozu brauchen Physiker das?
