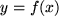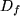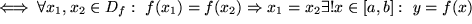Bijektiv:

Wie der Name "bijektiv" andeutet, nähern sich die Mathematiker dem Begriff der Eineindeutigkeit in zwei Schritten:

1) Zunächst nennen sie eine Abbildung injektiv, bei der gleiche Bildpunkte nur aus gleichen Urbildpunkten hervorgehen:

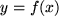injektiv in : ,

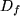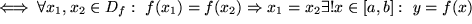oder äquivalent dazu: wenn verschiedene Urbilder auch immer zu verschiedenen Bildern führen:

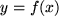injektiv in :

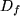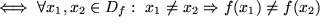
In diesem Fall hat die Gleichung 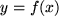) für alle 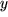höchstens eine Lösung , und jede Parallele zur 1-Achse schneidet den Graphen der Funktion höchstens einmal.

2) Dann betrachten sie in einem zweiten Schritt die für uns nicht so wichtige Menge, in der die Bildelemente liegen, und untersuchen, ob diese nur aus den Bildpunkten besteht oder noch weitere Punkte enthält. Falls die angegebene Bildmenge nur aus dem Wertevorrat besteht, nennen sie die Abbildung surjektiv :

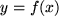surjektiv auf :

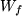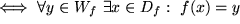
Dann hat die Gleichung 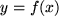für alle 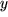wenigstens eine Lösung .

Also hat bei einer bijektiven Abbildung die Gleichung 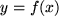genau eine Lösung und die Funktion ist umkehrbar.

Zurück zum Text