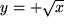Für alle eineindeutigen Funktionen, d.h. umkehrbar eindeutigen Abbildungen eines Definitionsbereichs
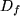 in einen Wertevorrat
in einen Wertevorrat
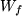 kann man durch Auflösen der Gleichung
kann man durch Auflösen der Gleichung
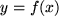 nach
nach
 Umkehrfunktionen
Umkehrfunktionen
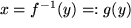 bilden, wobei Definitionsbereich
und Wertevorrat ihre Rollen vertauschen:
bilden, wobei Definitionsbereich
und Wertevorrat ihre Rollen vertauschen:
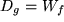 und
und
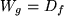 . Die Umkehrfunktion beschreibt
die Umkehrung der ursprünglichen Abbildung. Da die ursprüngliche Abbildung
. Die Umkehrfunktion beschreibt
die Umkehrung der ursprünglichen Abbildung. Da die ursprüngliche Abbildung
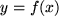 und die Rückabbildung
und die Rückabbildung
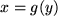 sich in ihrer Wirkung gerade aufheben,
gilt für die mittelbare Funktion
sich in ihrer Wirkung gerade aufheben,
gilt für die mittelbare Funktion
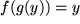 .
Daraus ist die oben angegebene Schreibweise
.
Daraus ist die oben angegebene Schreibweise
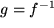 zu verstehen:
zu verstehen:
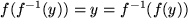 .
.
Im Sinne unserer physikalischen Definition der Funktion als Input-Output-Relation sind bei der
Umkehrfunktion Input und Output vertauscht, d.h. die Flußrichtungspfeile in unserem Bild bei
 und
und
 einfach umgekehrt.
einfach umgekehrt.
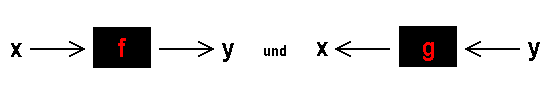
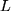 der Flüssigkeitssäule in einem engen
Glasrohr als Funktion der Temperatur
der Flüssigkeitssäule in einem engen
Glasrohr als Funktion der Temperatur
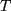 :
:
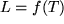 . Wenn wir das Glasrohr als Thermometer
zur Messung der Temperatur benutzen, beobachten wir die Länge der Flüssigkeitssäule und schließen daraus auf die
Temperatur
. Wenn wir das Glasrohr als Thermometer
zur Messung der Temperatur benutzen, beobachten wir die Länge der Flüssigkeitssäule und schließen daraus auf die
Temperatur
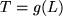 .
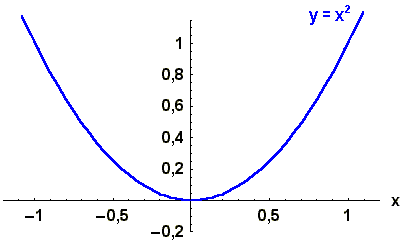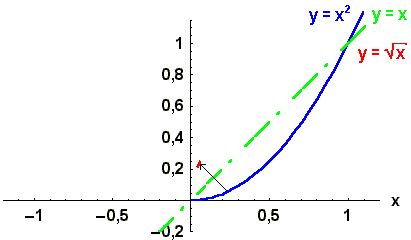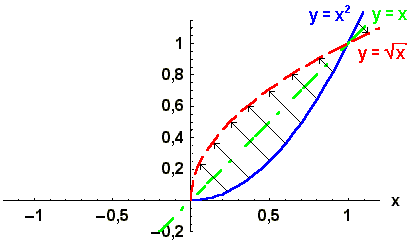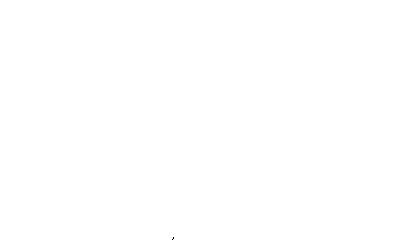
.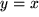 , d.h. der Winkelhalbierenden
des ersten und dritten Quadranten. Auf diese Weise erhält man aus jeder eineindeutigen Funktion eine neue Funktion.
, d.h. der Winkelhalbierenden
des ersten und dritten Quadranten. Auf diese Weise erhält man aus jeder eineindeutigen Funktion eine neue Funktion.
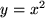 . Erst durch Einschränkung des
Definitionsbereichs auf
. Erst durch Einschränkung des
Definitionsbereichs auf
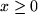 wird daraus
eine eineindeutige Funktion, die umkehrbar ist: die Umkehrfunktion ist eine neue Funktion für uns,
die Quadratwurzelfunktion
wird daraus
eine eineindeutige Funktion, die umkehrbar ist: die Umkehrfunktion ist eine neue Funktion für uns,
die Quadratwurzelfunktion
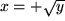 und nach Umbenennung der Variablen
und nach Umbenennung der Variablen
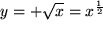 .
Durch die Bezeichnung mit dem Bruch im Exponent werden jetzt über unsere früheren Überlegungen hinausgehend
Potenzen auch für rationale Zahlen als Exponenten definiert, ohne dass sich an den Rechenregeln für Potenzen
etwas ändert.
.
Durch die Bezeichnung mit dem Bruch im Exponent werden jetzt über unsere früheren Überlegungen hinausgehend
Potenzen auch für rationale Zahlen als Exponenten definiert, ohne dass sich an den Rechenregeln für Potenzen
etwas ändert.