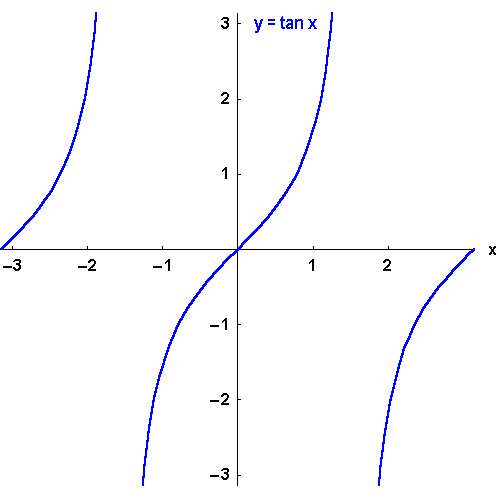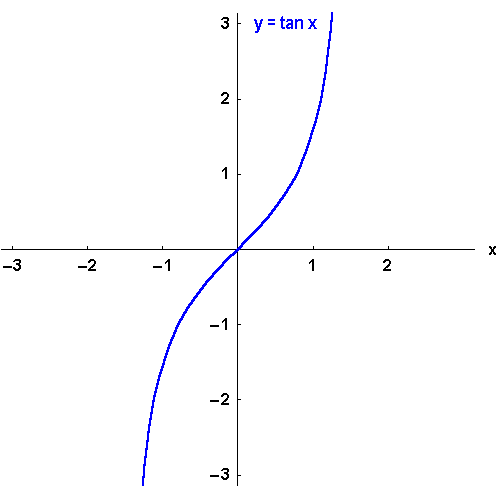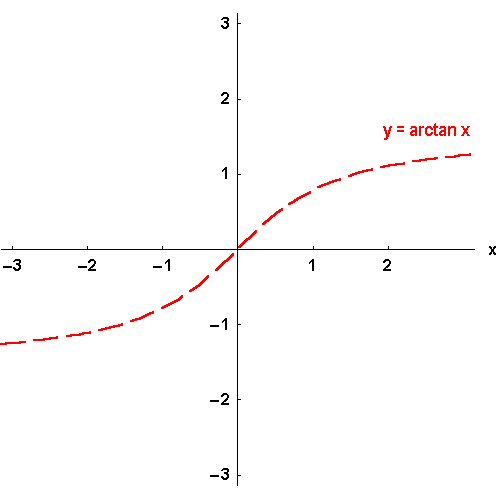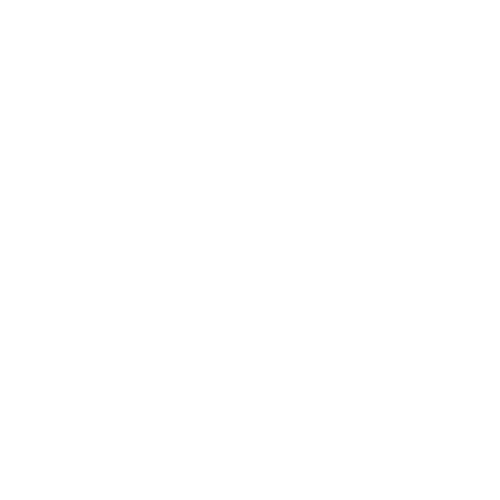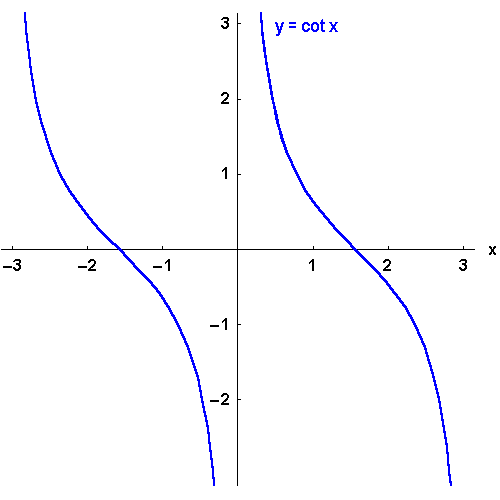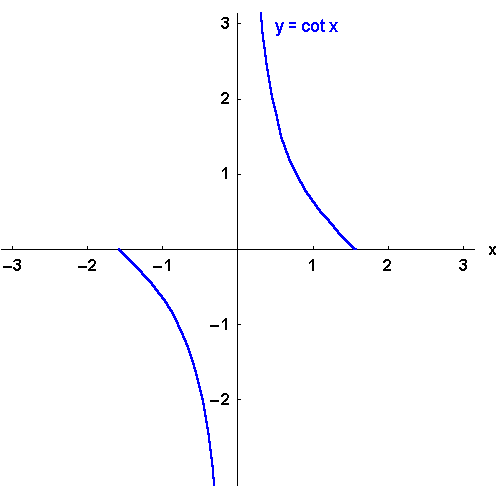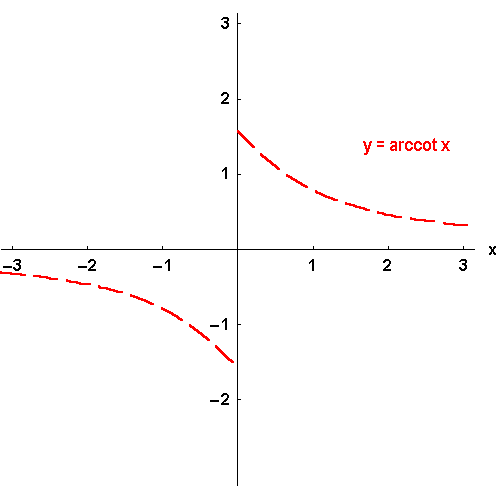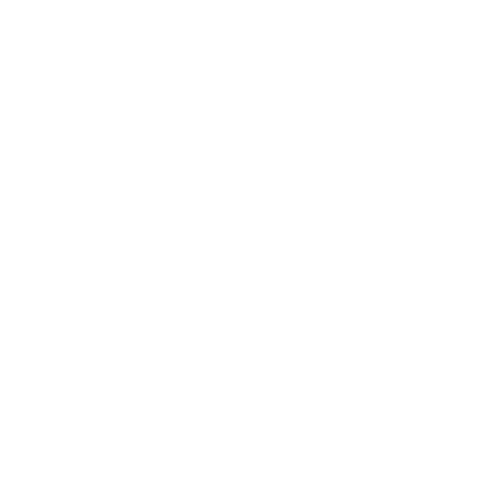Die trigonometrischen Funktionen
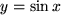oder
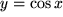sind periodisch in
mit der Periode
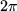und
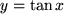oder
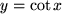mit der Periode
.
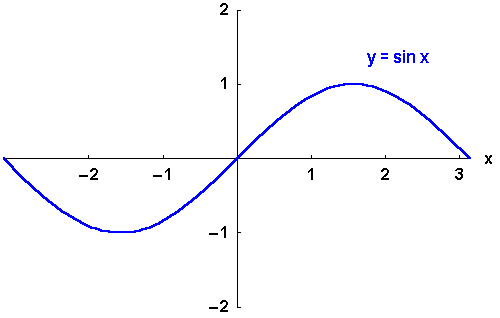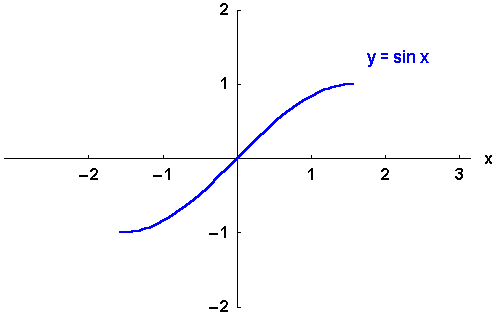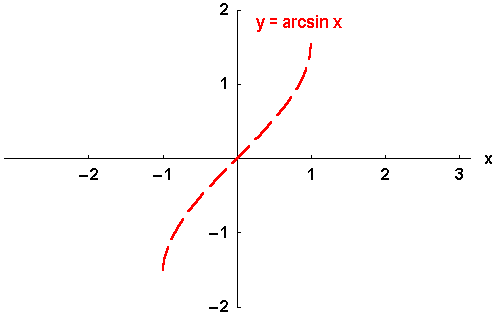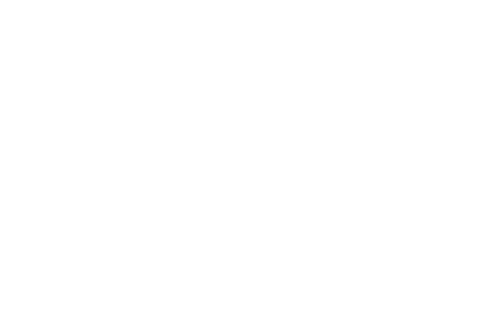
Sie sind also keine eineindeutigen Funktionen. Erst durch Einschränkung des Definitionsbereichs
kann die Eineindeutigkeit erreicht werden.
Für die ungeraden Funktionen
,
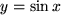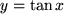und
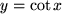wählt man meist
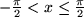, für das gerade
.
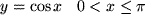Wegen der Periodizität kann man auch andere um Vielfache von
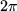verschobene Intervalle wählen. Hier ist eine gewisse Vorsicht beim Rechnen geboten,
insbesondere vor der Verwendung von Taschenrechnern sollte man sich über die Definitionsbereiche
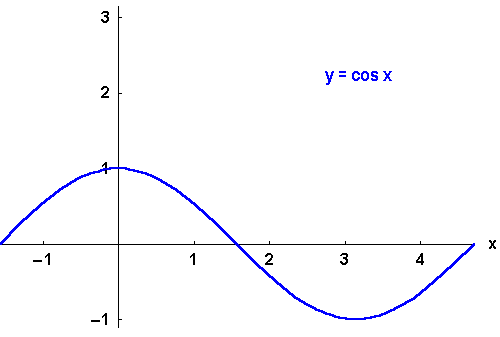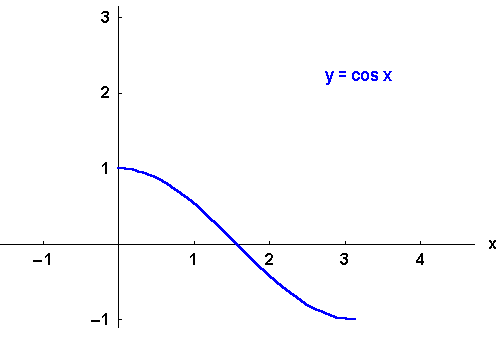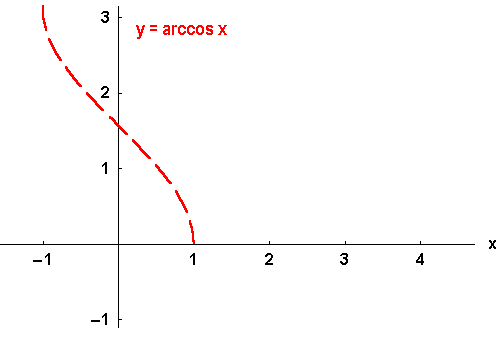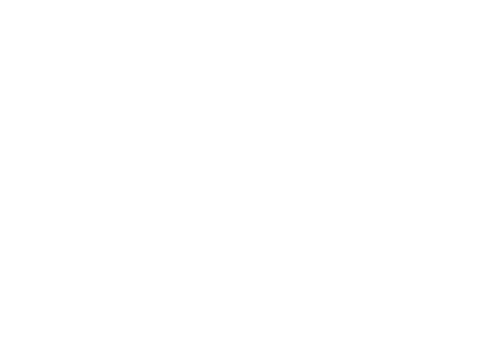
der Umkehrfunktionen informieren. Man nennt die Umkehrfunktionen der trigonometrischen Funktionen,
die zyklometrischen oder Arcus - Funktionen:
,
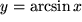
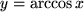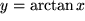und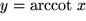
.
