|
Wir haben gesehen, dass der Differentialquotient einer Funktion  am Punkt am Punkt  eine schöne anschauliche Bedeutung hat: Er gibt die Steigung der Tangenten an den Graph der Funktion im Punkt eine schöne anschauliche Bedeutung hat: Er gibt die Steigung der Tangenten an den Graph der Funktion im Punkt  an. Man kann diese Tangenteneigenschaft auch noch folgendermaßen verstehen: an. Man kann diese Tangenteneigenschaft auch noch folgendermaßen verstehen:
Wir stellen uns die Aufgabe, eine durch eine Funktion 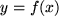 beschriebene ebene Kurve in der Umgebung eines Punktes beschriebene ebene Kurve in der Umgebung eines Punktes  möglichst gut durch eine Gerade möglichst gut durch eine Gerade 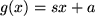 zu approximieren: Wir fordern dazu: zu approximieren: Wir fordern dazu:
1) Am Punkt  gelte gelte 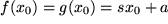 , woraus das absolute Glied , woraus das absolute Glied 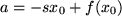 bestimmt werden kann. Eingesetzt ergibt das: bestimmt werden kann. Eingesetzt ergibt das: 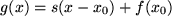 . Damit erhalten wir für die Abweichung der Näherungsgeraden . Damit erhalten wir für die Abweichung der Näherungsgeraden 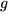 von der Kurve von der Kurve 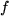 : :
mit der Entfernung der unabhängigen Variablen vom Approximationspunkt 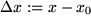 . .
2) Diese Abweichung der Näherungsgeraden 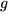 von der Kurve von der Kurve 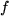 , gemessen in , gemessen in 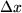
soll bei bester Approximation möglichst verschwinden bei Annäherung von  an an  , d.h. , d.h. 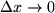 . Das bedeutet aber gerade: . Das bedeutet aber gerade:
 und folglich 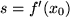 .
Wir erhalten also genau dann die beste lineare Approximation des Graphen der Funktion  in der Umgebung des Punktes in der Umgebung des Punktes  , wenn wir eine Gerade mit dem Differentialquotienten als Steigung wählen, und das ist natürlich gerade die Definition der Tangente. , wenn wir eine Gerade mit dem Differentialquotienten als Steigung wählen, und das ist natürlich gerade die Definition der Tangente.
|
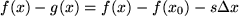
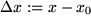 .
.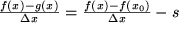
 und folglich
und folglich 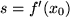 .
.
 am Punkt
am Punkt  eine schöne anschauliche Bedeutung hat: Er gibt die Steigung der Tangenten an den Graph der Funktion im Punkt
eine schöne anschauliche Bedeutung hat: Er gibt die Steigung der Tangenten an den Graph der Funktion im Punkt 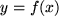 beschriebene ebene Kurve in der Umgebung eines Punktes
beschriebene ebene Kurve in der Umgebung eines Punktes 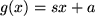 zu approximieren: Wir fordern dazu:
zu approximieren: Wir fordern dazu: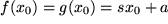 , woraus das absolute Glied
, woraus das absolute Glied 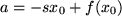 bestimmt werden kann. Eingesetzt ergibt das:
bestimmt werden kann. Eingesetzt ergibt das: 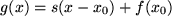 . Damit erhalten wir für die Abweichung der Näherungsgeraden
. Damit erhalten wir für die Abweichung der Näherungsgeraden 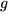 von der Kurve
von der Kurve 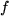 :
: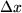
 an
an 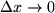 . Das bedeutet aber gerade:
. Das bedeutet aber gerade: