|
Differentiale:
Um mit dem wichtigen Begriff des Differentialquotienten noch vertrauter zu werden, wollen wir noch einen alternativen Zugang betrachten: den Begriff des Differentials. Es geschieht dabei nichts wesentlich Neues. Wir erhalten nur neue Einblicke in das Erreichte auch im Hinblick auf spätere Anwendungen und Erweiterungen, denn dieser Begriff kann leicht auf mehrere Dimensionen übertragen werden und wird erst dort seine ganze Kraft entfalten:
Wir vermeiden dabei bewußt den Grenzwert und schreiben den Differenzenquotienten als Gleichung: 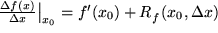 mit einem Rest mit einem Rest 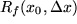 , der von der Funktion , der von der Funktion 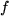 , der Stelle , der Stelle  und dem Intervall und dem Intervall 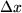 abhängt und mit abhängt und mit 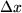 verschwindet. Multiplizieren wir diesen Differenzenquotienten mit dem Zuwachs der Variablen verschwindet. Multiplizieren wir diesen Differenzenquotienten mit dem Zuwachs der Variablen 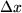 , so erhalten wir , so erhalten wir
den "wahren Zuwachs" unserer Funktion bei  : : 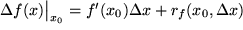 mit einem neuen Rest mit einem neuen Rest 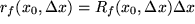 , der offensichlich noch stärker als , der offensichlich noch stärker als 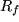 mit mit 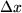 verschwindet. Wenn wir von diesem Rest absehen können, erhalten wir so für den wahren Zuwachs der Funktion verschwindet. Wenn wir von diesem Rest absehen können, erhalten wir so für den wahren Zuwachs der Funktion 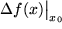 eine erste in eine erste in 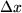 lineare Näherung, lineare Näherung,
den "linearen Anteil des Zuwachses der Funktion" 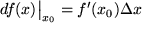 , der Differential genannt wird. , der Differential genannt wird.
Speziell für die Funktion 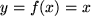 , die Winkelhalbierende, erhalten wir mit , die Winkelhalbierende, erhalten wir mit 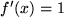 den linearen Anteil der linearen Funktion der unabhängigen Variablen: den linearen Anteil der linearen Funktion der unabhängigen Variablen: 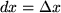 , der nicht notwendig infinitesimal sein muß und den wir oben einsetzen können, um mit der Lagrangeschen bzw. Leibnizschen Formulierung des Differentialquotienten zu erhalten: , der nicht notwendig infinitesimal sein muß und den wir oben einsetzen können, um mit der Lagrangeschen bzw. Leibnizschen Formulierung des Differentialquotienten zu erhalten:
|
Differential: 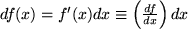 , linearer Anteil des Zuwachses der Funktion. , linearer Anteil des Zuwachses der Funktion.
|
Damit haben wir eine Gleichung, in der die Symbole 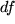 und und 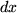 , die in der Leibnizschen Formulierung des Differentialquotienten zunächst nur als Quotient definiert waren, jetzt einzeln vorkommen und als "lineare Anteile des Zuwachses" auch als nichtinfinitesimale Größen definiert sind. Wegen dieser Möglichkeit ziehen wir die weitsichtige und suggestive Leibnizsche Schreibweise für den Differentialquotienten der Ihnen von der Schule her bekannten von Lagrange bei vielen Gelegenheiten vor. , die in der Leibnizschen Formulierung des Differentialquotienten zunächst nur als Quotient definiert waren, jetzt einzeln vorkommen und als "lineare Anteile des Zuwachses" auch als nichtinfinitesimale Größen definiert sind. Wegen dieser Möglichkeit ziehen wir die weitsichtige und suggestive Leibnizsche Schreibweise für den Differentialquotienten der Ihnen von der Schule her bekannten von Lagrange bei vielen Gelegenheiten vor.
|
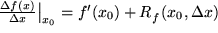 mit einem Rest
mit einem Rest 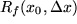 , der von der Funktion
, der von der Funktion 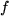 , der Stelle
, der Stelle  und dem Intervall
und dem Intervall 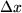 abhängt und mit
abhängt und mit 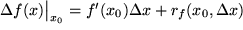 mit einem neuen Rest
mit einem neuen Rest 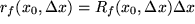 , der offensichlich noch stärker als
, der offensichlich noch stärker als 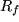 mit
mit 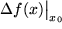 eine erste in
eine erste in 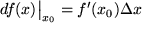 , der Differential genannt wird.
, der Differential genannt wird.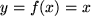 , die Winkelhalbierende, erhalten wir mit
, die Winkelhalbierende, erhalten wir mit 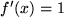 den linearen Anteil der linearen Funktion der unabhängigen Variablen:
den linearen Anteil der linearen Funktion der unabhängigen Variablen: 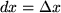 , der nicht notwendig infinitesimal sein muß und den wir oben einsetzen können, um mit der Lagrangeschen bzw. Leibnizschen Formulierung des Differentialquotienten zu erhalten:
, der nicht notwendig infinitesimal sein muß und den wir oben einsetzen können, um mit der Lagrangeschen bzw. Leibnizschen Formulierung des Differentialquotienten zu erhalten: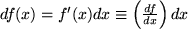 , linearer Anteil des Zuwachses der Funktion.
, linearer Anteil des Zuwachses der Funktion.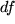 und
und 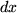 , die in der Leibnizschen Formulierung des Differentialquotienten zunächst nur als Quotient definiert waren, jetzt einzeln vorkommen und als "lineare Anteile des Zuwachses" auch als nichtinfinitesimale Größen definiert sind. Wegen dieser Möglichkeit ziehen wir die weitsichtige und suggestive Leibnizsche Schreibweise für den Differentialquotienten der Ihnen von der Schule her bekannten von Lagrange bei vielen Gelegenheiten vor.
, die in der Leibnizschen Formulierung des Differentialquotienten zunächst nur als Quotient definiert waren, jetzt einzeln vorkommen und als "lineare Anteile des Zuwachses" auch als nichtinfinitesimale Größen definiert sind. Wegen dieser Möglichkeit ziehen wir die weitsichtige und suggestive Leibnizsche Schreibweise für den Differentialquotienten der Ihnen von der Schule her bekannten von Lagrange bei vielen Gelegenheiten vor.