|
Unstetige Funktion differenzierbar?
Kann aber eine unstetige Funktion eventuell differenzierbar sein? Dazu untersuchen wir unser Muster einer unstetigen Funktion, die an der Stelle
 unstetige Heaviside-Funktion unstetige Heaviside-Funktion
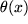 , um zu illustrieren, dass wir zurecht bei der Differenzierbarkeit die Stetigkeit nicht vorausgesetzt haben: , um zu illustrieren, dass wir zurecht bei der Differenzierbarkeit die Stetigkeit nicht vorausgesetzt haben:
Wir sehen leicht, dass der "Grenzwert von rechts"
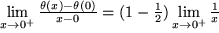 und der linksseitige und der linksseitige
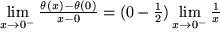 beide nicht existieren. beide nicht existieren.
Das könnte auch nicht dadurch behoben werden, dass man den zunächst etwas willkürlich erscheinenden Wert
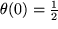 etwa zu etwa zu
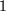 festlegt, denn dann würde zwar der rechtsseitige Grenzwert gleich festlegt, denn dann würde zwar der rechtsseitige Grenzwert gleich
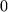 , aber der "Grenzwert von links" wäre weiterhin , aber der "Grenzwert von links" wäre weiterhin
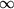 . Also ist unsere unstetige Musterfunktion an der Unstetigkeitsstelle irreparabel nicht differenzierbar, obwohl sie rechts und links davon eine horizontale Tangente besitzt. . Also ist unsere unstetige Musterfunktion an der Unstetigkeitsstelle irreparabel nicht differenzierbar, obwohl sie rechts und links davon eine horizontale Tangente besitzt.
|