Extrema:

Aus der Schule kennen viele von Ihnen die Anwendung dieser Deutung der ersten und zweiten Ableitungen einer Funktion aus der Kurvendiskussion:

Das Verschwinden der ersten Ableitung 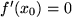an einer Stelle , das Kriterium für eine waagrechte Tangente in diesem Punkt, ist eine notwendige Vorausetzung für das Vorliegen eines lokalen Extremums. Hinreichend kann die Bedingung deshalb nicht sein, weil ja auch eine horizontale Wendetangente vorliegen könnte.

Hinreichende Bedingungen für ein lokales Maximum oder Minimum erhält man erst durch Betrachten der zweiten Ableitungen: 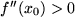bedeutet Linkskurve, also ein lokales Minimum, während 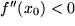auf eine Rechtkurve deutet und bei einem Maximum folgt.