In manchen Fällen kann oder will man die Ableitung einer Funktion nicht analytisch nach den Regeln des letzten Abschnitts berechnen, z.B. wenn man noch keine analytische Form für den Graph einer Funktion gefunden hat. Dann ist man auf die numerische Differentiation angewiesen.
Unsere Definitionsgleichung des Differentialquotienten aus Abschnitt 5.2:
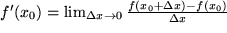
kann auch für die numerische Berechnung der Ableitung verwendet werden. Zum Punkt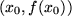 
sucht man dabei die Nachbarpunkte 
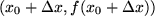, berechnet jeweils den Differenzenquotienten und läßt 
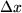gegen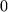 
gehen.
Da aber alle Computerzahlen nur mit einer bestimmten Genauigkeit (z.B. mit 8 Stellen) gespeichert werden, treten bei den Differenzen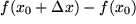 
Rundungsfehler auf, die zwar absolut immer gleich groß bleiben, aber relativ zum Wert der Differenz immer größer werden, so dass der Differenzenquotient mit kleiner werdendem 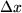immer genauer 
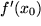approximiert, aber dann wegen der numerischen Rundungsfehler mit noch kleiner werdendem 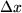größer wird. Es muß also ein Kompromiß gefunden werden. Eine bessere Approximation findet man, wenn man eine symmetrische Form der Definition wählt:
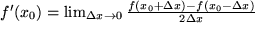
Mit Hilfe der Taylor-Entwicklung, die wir im nächsten Kapitel behandelten werden, kann man zeigen, dass der Fehler durch die Symmetrisierung von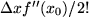 
auf die Größenordnung von 
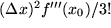reduziert wird, also quadratisch mit 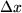kleiner wird.