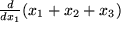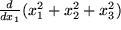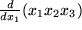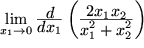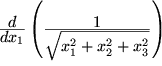Zur Motivation dieses Kapitels über die Differentiation haben wir eingangs bemerkt, dass viele Naturgesetzte sich als Differentialgleichungen schreiben lassen. Was ist das, eine Differentialgleichung?
Eine Differentialgleichung ist eine Beziehung zwischen einer gesuchten Funktion  und ihren Ableitungen
und ihren Ableitungen 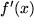 ,
, 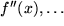
Wenn man z.B. die Auslenkung eines an einer Spiralfeder von der Decke herabhängenden Gewichts aus seiner Ruhelage mit 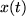 bezeichnet, wobei
bezeichnet, wobei 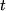 die Zeit darstellt, dann folgt, wenn man vom Luftwiderstand absieht, aus Newtons zweitem Gesetz folgende Differentialgleichung:
die Zeit darstellt, dann folgt, wenn man vom Luftwiderstand absieht, aus Newtons zweitem Gesetz folgende Differentialgleichung:
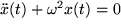 mit einer Konstanten
mit einer Konstanten 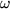 .
.
Wie die meisten Differentialgleichungen der Physik ist sie "zweiter Ordnung", d.h. der höchste auftretende Differentialquotient ist eine zweite Ableitung der gesuchten Funktion. Während bei einer "normalen" Gleichung, z.B. mit einer Unbekannten etwa 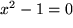 , die Zahlenwerte für
, die Zahlenwerte für  , hier
, hier 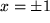 , gesucht werden, sind bei dieser "Differentialgleichung" jetzt Funktionen der Zeitvariablen
, gesucht werden, sind bei dieser "Differentialgleichung" jetzt Funktionen der Zeitvariablen 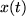 als Lösungen gesucht. Man sieht sehr schnell, dass
als Lösungen gesucht. Man sieht sehr schnell, dass 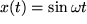 eine Lösung ist, da
eine Lösung ist, da 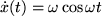 und folglich
und folglich 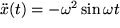 . Aber ist das die einzige Lösung? Mit solchen Fragen werden Sie sich noch viel beschäftigen.
. Aber ist das die einzige Lösung? Mit solchen Fragen werden Sie sich noch viel beschäftigen.
|
Aufgabe 5.9: Physikalische Differentiationen Bilden sie die erste Der Vergleich von
|
Sie werden später bei den Funktionen mehrerer Variabler noch kompliziertere Differentiationsoperationen kennen lernen: mit Hilfe der sogenannten partiellen Ableitungen werden Sie Gradienten von Skalarfeldern sowie die Divergenz oder die Rotation von Vektorfeldern bilden. Wenn es aber darum geht, Zahlen auszurechnen, werden Sie nichts anderes benötigen als das, was Sie hier gelernt haben.
|
Aufgabe 5.10: Partielle Ableitungen Die Änderung von Funktionen mehrerer Variablen, z.B. von Feldern der drei Ortsvariablen
|
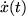 und die zweite
und die zweite 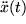 Ableitung folgender Funktionen
Ableitung folgender Funktionen  ,
, 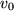 ,
, 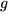 ,
, 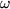 ,
, 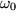 ,
, 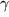 ,
, 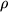 ,
, 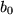 ,
, 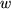 ,
, 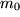 und
und 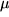 :
: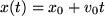
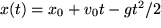
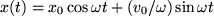
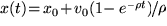
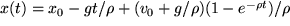

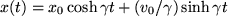
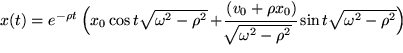
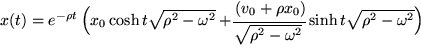
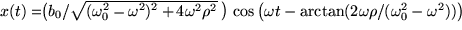
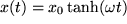
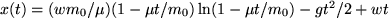
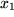 ,
, 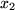 ,
, 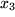 , werden Sie später durch sogenannte partielle Differentialquotienten beschreiben, bei denen jeweils nur eine der Variablen, z.B.
, werden Sie später durch sogenannte partielle Differentialquotienten beschreiben, bei denen jeweils nur eine der Variablen, z.B. 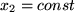 und
und 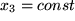 . Ohne weiteres Verständnis der tieferen Hintergründe können Sie diese "partiellen" Ableitungen, für die dann eine neue Bezeichnung (Nabla:
. Ohne weiteres Verständnis der tieferen Hintergründe können Sie diese "partiellen" Ableitungen, für die dann eine neue Bezeichnung (Nabla: 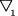 ) eingeführt werden muß, nach dem oben Gelernten schon jetzt berechen. Dazu verfahren Sie genauso wie oben mit den verschiedenen Konstanten. Berechnen Sie zum Beispiel:
) eingeführt werden muß, nach dem oben Gelernten schon jetzt berechen. Dazu verfahren Sie genauso wie oben mit den verschiedenen Konstanten. Berechnen Sie zum Beispiel: