Wir betrachten zuerst noch einmal das einfachste aller Polynome, die geometrische Summe,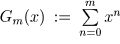 
mit den Koeffizienten 
für alle nichtnegativen ganzen Zahlen n und die zugehörige Potenzreihe, die geometrische Reihe:
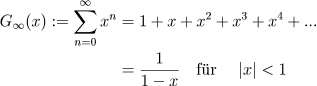
Darin haben wir bereits einen Prototyp für unseren Wunschtraum: Die rationale Funktion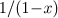 
wird im offenen Intervall 
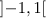um die Stelle 
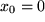herum durch eine Potenzreihe, die geometrische Reihe 
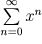, dargestellt, d.h. durch die Summe aus der Konstanten eins, der winkelhalbierenden Geraden, der Normalparabel, einer Funktion dritten Grades, usw. angenähert. Diese Reihe hat zwar unendlich viele Glieder; sie sind jedoch allein durch Addition und Multiplikation berechenbar, und je nach Genauigkeitsanforderungen reichen schon wenige Glieder aus. Allerdings existiert die Darstellung nur im Intervall 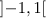, während die Funktion 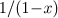überall außer für 
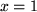definiert ist.
Dieses Beispiel und Vorbild macht uns Mut zu folgenden Fragen:
2) Wie erhält man die zugehörigen Koeffizienten
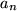?3) Wie viele verschiedene solche Reihen gibt es für eine Funktion ?
4) Wie gut ist die Konvergenz bzw. wie groß ist der Näherungfehler beim Abbruch der Reihe ?