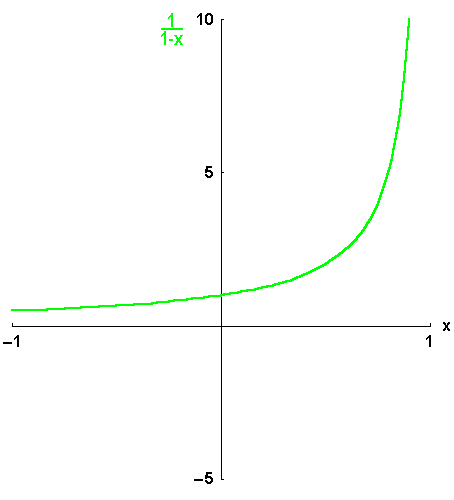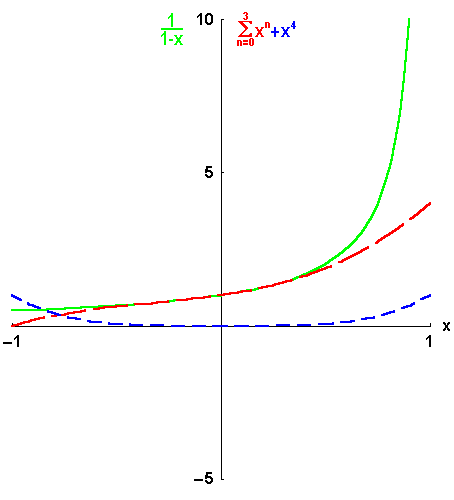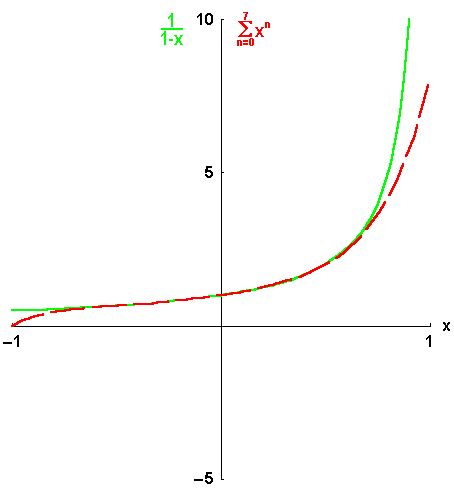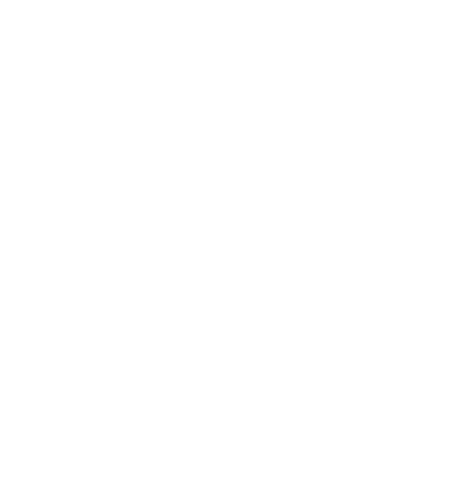
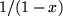Ehe wir uns mit der Existenzfrage beschäftigen, wollen wir uns den Fragen 2) und 3) zuwenden: Um Information über die möglichen Eigenschaften der gesuchten Entwicklung zu erhalten, wollen wir zunächst einmal annehmen, wir hätten schon eine Potenzreihe:
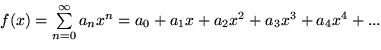 mit
mit 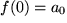
gefunden, die die betrachtete Funktion  in einem Intervall z.B. für
in einem Intervall z.B. für 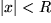 um den Nullpunkt herum darstellt. Da alle Funktionen unserer Grundausstattung unendlich oft differenzierbar sind, können wir die Ableitungen der Potenzreihe gliedweise der Reihe nach berechnen:
um den Nullpunkt herum darstellt. Da alle Funktionen unserer Grundausstattung unendlich oft differenzierbar sind, können wir die Ableitungen der Potenzreihe gliedweise der Reihe nach berechnen:
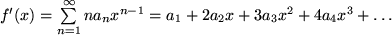 mit
mit  , also
, also 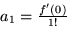
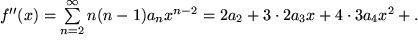 mit
mit 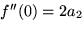 , also
, also 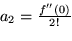
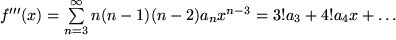 mit
mit  , also
, also 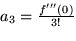
Allgemein:
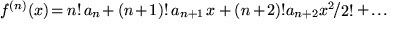 mit
mit 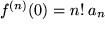 , also
, also 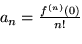 .
.
Wir erhalten so die gesuchten Koeffizieneten 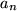 aus den Ableitungen
aus den Ableitungen 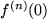 der darzustellenden Funktion an der Entwicklungsstelle
der darzustellenden Funktion an der Entwicklungsstelle 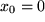 . Falls also eine Potenzreihen-Darstellung unserer Funktion existiert, hat sie folgende Form und wir nennen sie:
. Falls also eine Potenzreihen-Darstellung unserer Funktion existiert, hat sie folgende Form und wir nennen sie:
|
TAYLOR-REIHE: |
Nach der angegebenen Konstruktion sind die Koeffizienten überdies eindeutig, so dass wir auch die Frage 3) beantwortet haben.
Unsere Überlegungen zeigen uns auch, dass die darzustellende Funktion notwendigerweise beliebig oft differenzierbar sein muß, wenn eine Taylor-Reihe existieren soll.
Dass diese notwendige Voraussetzung nicht hinreichend für die Existenz der Taylor-Reihe ist, sieht man aus folgendem Gegenbeispiel: Die unten abgebildete Funktion, 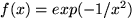 für
für 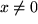 und
und  , ist zwar überall unendlich oft differenzierbar, alle ihre Ableitungen
, ist zwar überall unendlich oft differenzierbar, alle ihre Ableitungen 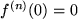 verschwinden jedoch an der Stelle
verschwinden jedoch an der Stelle  , so dass keine Taylor-Reihe um
, so dass keine Taylor-Reihe um 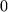 gebildet werden kann.
gebildet werden kann.
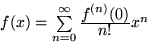
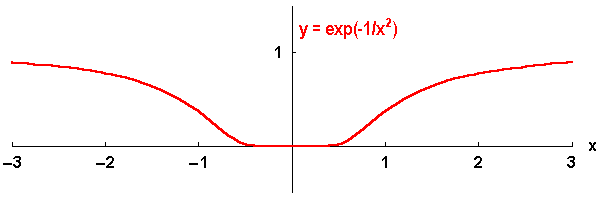
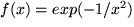 für
für 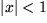 .
.