Die Funktionen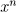 
mit natürlichen Exponenten 
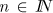sind bereits einfache Spezialfälle von Potenzreihen mit einem einzigen Term. Potenzen von 
mit negativen Exponenten sind für 
gar nicht definiert.
Jedoch die allgemeine binomische Reihe mit reellem Exponenten 
kann entwickelt werden:
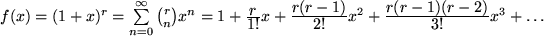
mit dem verallgemeinerten Binomialkoeffizient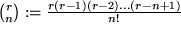 
und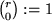 
.
Zum Beweis: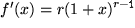 
,
,
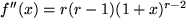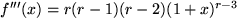, ... usw.
allgemein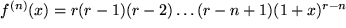 
mit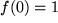 
,
,
,
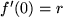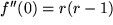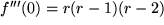, ... usw.
allgemein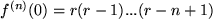 
,
insgesamt: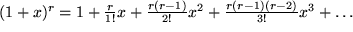 
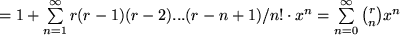
Einige Spezialfälle sind von besonderer Wichtigkeit:
Zunächst finden wir für natürliche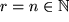 
unsere früher abgeleitete binomische Formel wieder für den Spezialfall 
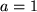und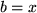 
, da die Potenzreihe im Fall natürlicher Exponenten abbricht:
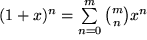
Für negative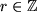 
ergibt sich, z.B. für 
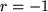erneut die alternierende geometrische Reihe
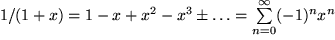
und für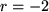 
deren negative Ableitung:
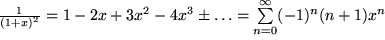
Für gebrochene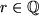 
, z.B. 
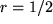oder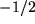 
erhalten wir die häufig gebrauchten Reihenentwicklungen der Quadratwurzel im Zähler bzw. Nenner:
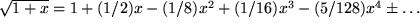bzw.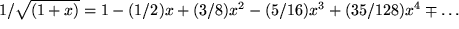
|
Aufgabe 6.2: Berechnen Sie die Taylor-Reihen von |
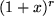für 
, 
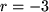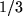und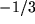 
.