Besonders einfach zu berechnen ist die Reihe der natürlichen Exponentialfunktion:
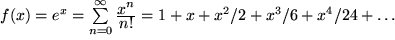
denn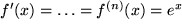 
, mit 
.
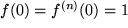Speziell für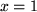 
erhalten wir 
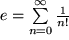, die Reihe, mit der wir die Zahl e definiert hatten.
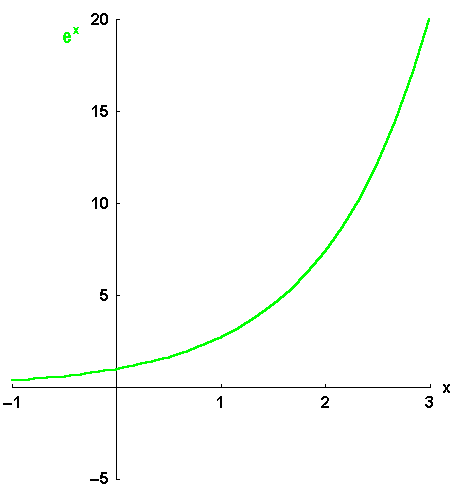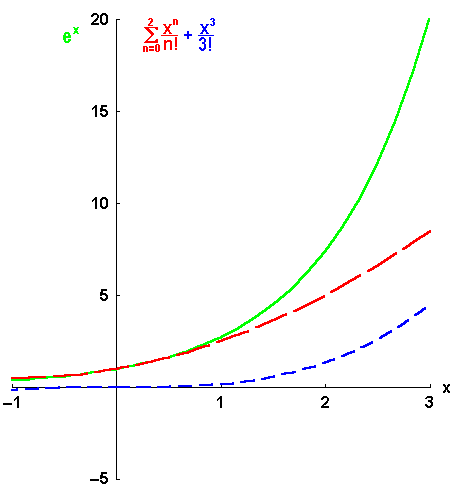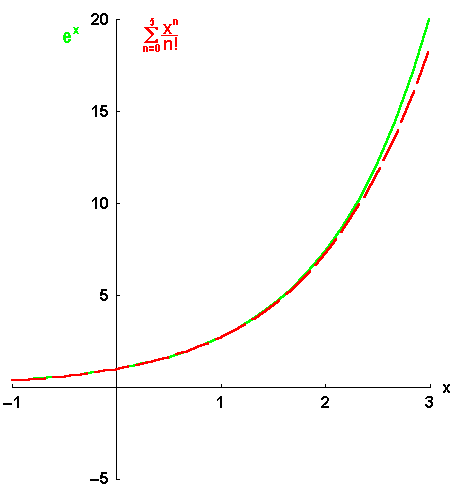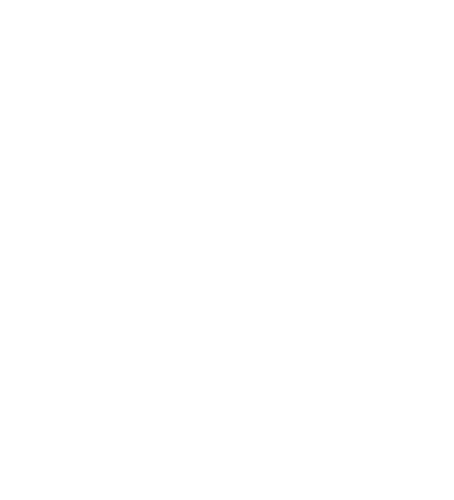
Bild 6.4: Aufbau der Taylor-Entwicklung für die Exponentialfunktion
Die Umkehrfunktion der natürlichen Exponentialfunktion, der natürliche Logarithmus kann nicht um 
entwickelt werden, da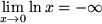 
ist. Es gibt jedoch eine Entwicklung für
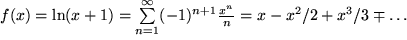
Speziell für 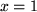folgt
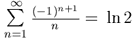, wie in Abschnitt 3.5 schon vorweg verraten.
|
Aufgabe 6.4: Beweisen Sie diese Taylor-Entwicklung für |
. In der folgenden Tabelle haben wir für einige besonders häufig auftretenede Funktionen jeweils die ersten beiden Terme der Taylor-Entwicklungen zum Auswendiglernen zusammengestellt.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
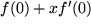
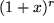
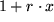
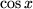
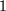
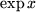
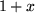
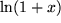
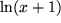