Mit diesen wenigen Taylor-Reihen erhalten wir leicht eine große Zahl weiterer Entwicklungen, wenn wir berücksichtigen, was wir früher über das Rechnen mit Reihen gelernt haben. Als Beispiel für eine Linearkombination zweier Taylor-Reihen berechnen wir die Entwicklung des Sinus hyperbolicus:
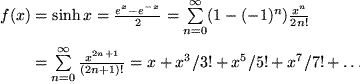
Überraschenderweise ist das genau die Taylor-Reihe des trigonometrischen Sinus, nur ohne die Vorzeichenwechsel, was ein Licht auf die Namensgebung wirft.
Ein weiteres Beispiel zeigt, wie man die Taylor-Reihe des Produkts zweier Funktionen aus den Taylor-Reihen der Faktoren erhält, indem man die beiden Reihen einfach multipliziert und das Ergebnis nach Potenzen sortiert:
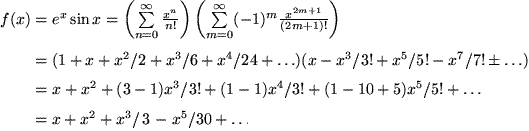
Auch bei verketteten Funktionen, bei denen man die Taylor-Reihen der inneren und äußeren Funktion kennt, ist es oft einfacher, diese ineinander einzusetzen, als die Differentialquotienten direkt zu berechnen: Etwa
|
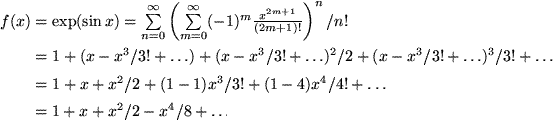
Aufgabe 6.5: Berechnen Sie die Taylor-Entwicklungen folgender Funktionen
|
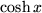
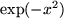
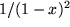durch gliedweise Differentiation der geometrischen Reihe. 
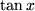durch Division der Reihen 
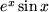direkt durch Berechnung der Ableitungen 
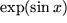ebenfalls direkt.