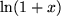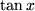Bereits bei unserem Vorbild, der geometrischen Reihe, war die Gültigkeit der Reihenentwicklung auf das Intervall 
um den Nullpunkt herum beschränkt. Auch bei den anderen Taylor-Reihen, selbst wenn die darzustellenden Funktionen in einem abgeschlossenen Intervall (d.h. einschließlich der Randpunkte) unendlich oft differenzierbar sind, ist die Konvergenz im allgemeinen auf das Innere eines zum Nullpunkt symmetrischen Intervalls beschränkt: 
. Die Zahl R wird "Konvergenzradius" genannt, wobei das Wort "Radius" erst in der Funktionentheorie, d.h. bei Potenzreihen von komplexen Zahlen verständlich wird. Innerhalb dieses durch R begrenzten symmetrischen Konvergenzbereichs konvergieren alle Taylor-Entwicklungen allerdings dann sogar absolut. Außerhalb, d.h. für 
, sind sie divergent. Die Konvergenz in den beiden Randpunkten muß in jedem Einzelfall genauer untersucht werden.
Die Mathematiker stellen uns (durch Vergleich z.B. mit der geometrischen Reihe) Methoden bereit, um den Konvergenzradius zu bestimmen. Wir wollen nur eine dieser hinreichenden Bedingungen für die absolute Konvergenz einer Reihe 
hier angeben, nämlich das von D'Alembert stammende Quotienten-Kriterium, nach dem der Konvergenzradius folgendermaßen geschrieben werden kann:
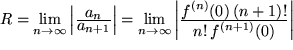
Damit erhalten wir: z.B. für die allgemeine Binomialreihe:
jedoch für den trigonometrischen und den hyperbolischen Sinus:
sowie für die Exponentialfunktion:
d.h. die ganze reelle Achse als Konvergenzgebiet.
sagen?
und 
