Nach den Ergebnissen aus den letzten Abschnitten bleibt nur noch die Frage 4) nach der Güte der Konvergenz: Auch wenn wir der Konvergenz der Reihe sicher sind, ist es natürlich nicht unwesentlich, wie groß der Fehler wird, wenn man statt der unendlichen Potenzreihe nur ein
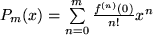
verwendet. Anstatt das Restglied 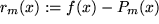 genau zu berechnen, wollen wir nur eine Formel angeben, die aus dieser Rechnung hervorgeht und dazu dienen kann,
genau zu berechnen, wollen wir nur eine Formel angeben, die aus dieser Rechnung hervorgeht und dazu dienen kann, 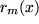 abzuschätzen, die sogenannte
abzuschätzen, die sogenannte
|
Lagrange-Form des Restglieds |
Der Ausdruck setzt uns zunächst in Erstaunen, denn er hat die leicht einprägsame Form des (m+1)-ten Gliedes der Reihe, d.h. des ersten weggelassenen Terms, soll jedoch für die ganze Restreihe stehen. Dieser scheinbare Widerspruch wird dadurch aufgeklärt, dass die (m+1)-te Ableitung im Restglied nicht wie beim (m+1)-ten Glied der Reihe am Entwicklungspunkt 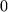 zu nehmen ist, sondern an einer unbekannten Zwischenstelle
zu nehmen ist, sondern an einer unbekannten Zwischenstelle 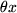 zwischen dem Entwicklungspunkt
zwischen dem Entwicklungspunkt 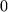 und der interessierenden Stelle
und der interessierenden Stelle  , ausgedrückt durch die unbekannte Zahl
, ausgedrückt durch die unbekannte Zahl 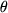 mit
mit 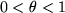 . Wegen dieser Unbekanntheit von
. Wegen dieser Unbekanntheit von 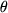 läßt sich das Restglied im allgemeinen nicht ausrechnen, sondern nur
läßt sich das Restglied im allgemeinen nicht ausrechnen, sondern nur
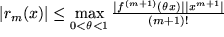 .
.
Aus dieser Abschätzungsformel sieht man, dass der Fehler klein wird mit der (m+1)-ten Potenz des Abstands der untersuchten Stelle  vom Entwicklungspunkt
vom Entwicklungspunkt 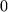 , dass es also günstig ist, mit dem Entwicklungspunkt möglichst nahe an den interessierenden Punkt heranzugehen.
, dass es also günstig ist, mit dem Entwicklungspunkt möglichst nahe an den interessierenden Punkt heranzugehen.
Als Beispiel wollen wir 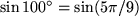 bis auf
bis auf 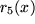 berechnen mit der in Abschnitt 6.4.2 gewonnen Taylor-Reihe um den Punkt
berechnen mit der in Abschnitt 6.4.2 gewonnen Taylor-Reihe um den Punkt 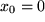
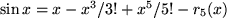 :
:
Wir erhalten: 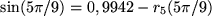 , wobei die Restgliedabschätzung mit
, wobei die Restgliedabschätzung mit 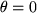 ergibt:
ergibt:
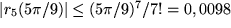
Der exakte Wert ist 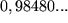 und seine Differenz zum Näherungswert beträgt
und seine Differenz zum Näherungswert beträgt 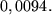 .
.
|
Aufgabe 6.10: Berechnen Sie die quadratischen Glieder der Taylor-Entwicklungen und die Restglieder |
|
Aufgabe 6.11: Berechnen Sie |
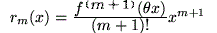 , wobei
, wobei 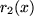 in unserer kleinen Tabelle aus
in unserer kleinen Tabelle aus 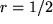 ,
, 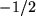 und
und 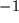 und schätzen Sie die Fehler ab: Bei welchen Stellen
und schätzen Sie die Fehler ab: Bei welchen Stellen 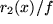 jeweils 1% bzw. 10%?
jeweils 1% bzw. 10%? 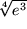 mit der Taylor-Reihe um
mit der Taylor-Reihe um 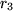 .
.