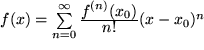Nachdem wir gesehen haben, wie sehr es bei der Anwendung der Taylor-Entwicklungen zur Berechnung von Funktionswerten in der Nähe von Entwicklungspunkten, an denen die Funktion bekannt ist, auf die Nähe zur Entwicklungsstelle ankommt, wenden wir uns schließlich dem Problem der geschickten Wahl der Entwicklungsstelle 
zu, die wir zunächst immer speziell gleich 
gesetzt haben, was die Mathematiker Maclaurin-Form der Entwicklung nennen.
Wir erhalten die allgemeine Taylor-Entwicklung um eine Stelle aus unserer bisherigen Form ganz einfach, indem wir 
überall durch 
setzen und die erhaltene Funktion von 
in der Umgebung von 
entwickeln. So ergibt sich für unendlich oft differenzierbare Funktionen 
die Form und Eindeutigkeit der allgemeinen
|
Taylor-Entwicklung um den Punkt |
für den Konvergenzradius R das hinreichende Quotienten-Kriterium:
und für den Fehler beim Abbrechen nach dem m-ten Glied: die
|
Lagrange-Form des Restglieds |
wieder mit 
.Als Beispiel entwickeln wir die Sinus-Funktion 
jetzt um den Punkt 
:
Zum Beweis: 
, 
, 
, 
, ...
mit 
, 
, 
, 
, 
, ...
insgesamt: 
mit dem Konvergenzradius 
.
Wir wollen sogleich überprüfen, wie das näher bei 
liegende Entwicklungszentrum 
unsere in Abschnitt 6.7 mit dem Entwicklungszentrum 
durchgeführte Berechnung von 
verbessert:
Wir erhalten: 
, wobei die Restgliedabschätzung mit 
ergibt
Das ist zu vergleichen mit der früher erhaltenen Fehlerabschätzung von 
, d.h. durch die günstigere Wahl des Entwicklungszentrums konnte der Fehler bei vergleichbarem Rechenaufwand um mehr als vier Größenordnungen herabgesetzt werden.
Für andere gesuchte Zwischenwerte können wir den Sinus auch um 
entwickeln:
denn , , , , ...
mit 
, 
, 
, 
, 
, ...
insgesamt: 
mit dem Konvergenzradius 
Jetzt können wir auch eine Entwicklung des natürlichen Logarithmus angeben etwa um 
:
Wenn wir darin durch 
ersetzen gelangen wir wieder zu unserer früheren Taylor-Entwicklung von 
um den Punkt .
|
Aufgabe 6.12: Bestimmen Sie die Taylor-Entwicklungen und Konvergenzbereiche von:
|
um den Punkt 
um den Punkt 
um den Punkt |
Aufgabe 6.13: Berechnen Sie |
bis auf 
, jetzt aber mit der Taylor-Reihe um Sie werden im Verlauf Ihres Studiums noch viele andere Entwicklungen kennen lernen und selbst durchführen. Auch für Felder gibt es Taylor-Entwicklungen, z.B. die berühmte Multipol-Entwicklung. Sie werden die in den Naturwissenschaften häufigen periodischen Funktionen nach Fourier "im quadratischen Mittel" mit Cosinus und Sinus als Basisfunktionen entwickeln und später auch nichtperiodische Funktionen mit Hilfe der Exponentialfunktion "nach Fourier transfomieren". Komplexe Funktionen können sogar in einer gewissen Umgebung von bestimmten Singularitäten nach Laurent entwickelt werden. Schließlich werden Sie in der Quantenmechanik verschiedene störungstheoretische Entwicklungen um die wenigen exakt lösbaren Systeme durchführen, wie den harmonischen Oszillator. Die theoretische Physik ist zu einem beträchtlichen Teil die hohe Kunst des Entwickelns.