Das zweite Standbein der mathematischen Methoden für alle Naturwissenschaften ist die Integralrechnung. In gewissem Sinn ist die Integration die Umkehrung der Differentiation. Während diese einer Funktion 
ihre Steigung 
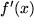zuordnet, beschäftigt sich die Integralrechnung mit Problemen, bei denen etwas über die Steigung einer Funktion bekannt ist und Funktionen mit dieser Steigung gesucht werden. Diese Aufgabe ist viel schwieriger als die der Differentiation, hat aber eine zentrale Bedeutung in den Naturwissenschaften. Es hat sich nämlich herausgestellt, dass die Grundgesetze der Mechanik, der Elektrodynamik und der Quantenmechanik in Form von Differentialgleichungen formuliert werden können, die Aussagen über die Ableitungen von Funktionen machen. Z.B. sagt das zweite Newtonsche Gesetz über die Bahnkurve 
eines Teilchens unter dem Einfluss einer Kraft K etwas über die zweite Ableitung, also die Beschleunigung:
Für eine gegebene Kraft z.B. die Schwerkraft oder eine elektrische Kraft soll daraus die Bahnkurve ermittelt werden. Integrieren heißt da einfach, Lösen der Grundgleichungen bzw. Anwenden der Theorie auf die verschiedenen in der Praxis vorliegenden Fälle.
In den vorhergehenden Kapiteln haben Sie das Handwerk des Differenzierens gelernt und eingeübt. Es ist eigentlich nicht so schwierig, wenn man einige Regeln beherzigt. Das Integrieren dagegen ist eine "Kunst", wie Sie bald sehen werden. Aber wie noch kein Künstler vom Himmel gefallen ist, sondern sein Talent erst durch Lernen, Sammeln von Erfahrungen und Üben entwickeln muß, so ist es auch beim Integrieren. Dazu sollen die nächsten Abschnitte Ihnen Gelegenheit geben.