7 Integration

7.1 Arbeit

Wir betrachten wieder zunächst die gleichförmige Bewegung eines Massenpunkts auf einer Geraden, z.B. den Schwerpunkt eines Autos auf einer Autobahn. Nachdem wir die erste Frage nach der Geschwindigkeit mit Hilfe der Differentialrechnung beantwortet haben, fragen wir mit den Physikern eine Schicht tiefer nach dem Grund: Warum bewegt sich das Auto auf dem geraden ebenen Autobahnabschnitt mit der beobachteten gleichförmigen Geschwindigkeit? Klarerweise ist die Ursache der gleichförmigen geradlinigen Bewegung nach Newton eine Kraft, und zwar die Kraft 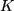, mit welcher der Motor den Wagen gegen Trägheit, Wind und andere Reibungsverluste vorantreibt. Spätestens beim Tanken kommt dann die Frage nach der Arbeit , die der Motor auf der zurückgelegten Strecke 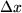geleistet hat. Diese Arbeit ist umso größer, je größer die benötigte Kraft war, und ist außerdem der zurückgelegten Wegstrecke 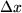proportional, ja sie ist genau gleich dem Produkt dieser beiden Größen: 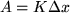, geometrisch gleich der Rechtecksfläche aus 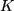mal 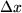, wenn wir etwa in einem kartesischen, d.h. rechtwinkligen Koordinatensystem den zurückgelegten Weg in Richtung der 1-Achse und die jeweils wirkende Kraft 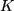in Richtung der 2-Achse auftragen.

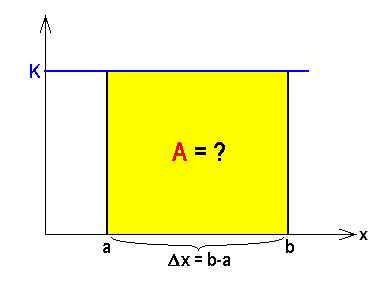
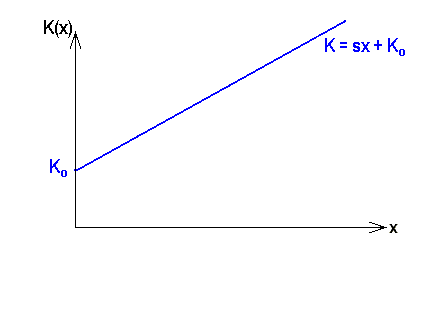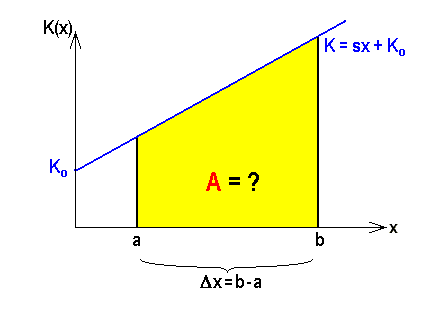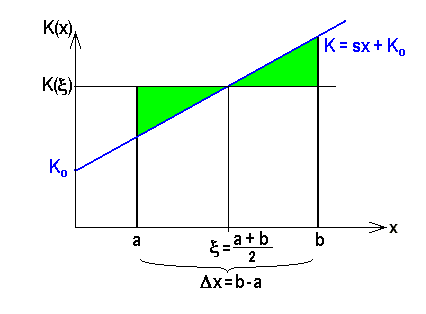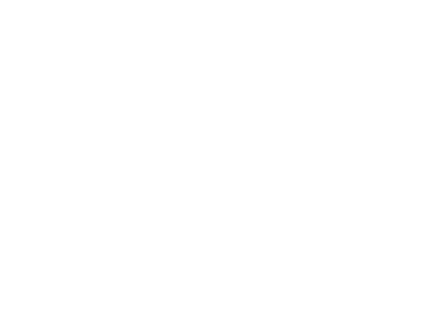
Bild 7.1: Konstante Kraft als Funktion der zurückgelegten Wegstrecke von bis 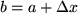. Die gelbe Rechteckfläche ist proportional der Arbeit .

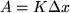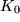Nach diesem idealisierten Fall einer konstant wirkenden Kraft gehen wir sogleich zu dem realistischeren Fall über, dass die Kraft sich auf der Strecke ändert, z.B. durch Gasgeben von einem Anfangswert linear anwächst: :

Bild 7.2: Linear vom Anfangswert nach anwachsende Kraft über dem zurückgelegten Weg zwischen den Punkten und .

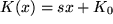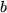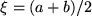Aus dem Bild sehen wir sofort, wie wir uns behelfen, wenn beim Tanken wieder die Frage nach der auf der ganzen Strecke geleisteten Arbeit auftaucht. Wir nehmen den Mittelwert zwischen dem Startpunkt 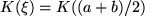und dem Endpunkt , lesen den entsprechenden Funktionswert der Kraft ab und multiplizieren diesen mit der zurückgelegten Wegstrecke :

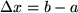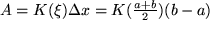
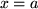Damit haben wir die physikalische Frage nach der Arbeit auf die geometrische Fragestellung nach der "Fläche unter der Kraftgeraden über dem Intervall ", genauer nach dem Inhalt der Fläche zurückgeführt, die von einer Funktion nach oben, der Geraden nach links, der Geraden 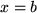nach rechts und der 1-Achse 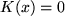nach unten begrenzt wird. Die weitergehende Frage nach der Arbeit bei einer nach einer beliebigen Funktion variablen Kraft ist damit zurückgeführt auf das mathematische Problem der Bestimmung des Flächeninhalts eines Rechtecks, bei dem eine (hier die obere) Seite durch eine krumme Linie ersetzt ist. Wir wollen im folgenden sogleich diese allgemeinere mathematische Fragestellung untersuchen und einer Lösung zuführen, die dann auch alle Wünsche der Physiker nach der Arbeit und darüber hinaus noch viele andere Wünsche erfüllt.