Der Einfachheit halber teilen wir das Intervall der Länge
Berechnung eines Integrals nach der Definition:
Nach dieser komplizierten Definition des Grenzübergangs verlangt man natürlich als erstes ein Beispiel: Wir wollen dazu die Funktion ![]() und das Intervall
und das Intervall ![]() wählen:
wählen:
Der Einfachheit halber teilen wir das Intervall der Länge ![]() durch
durch ![]() äquidistante Zwischenstellen
äquidistante Zwischenstellen ![]() in
in ![]() Intervalle der einheitlichen Länge
Intervalle der einheitlichen Länge ![]() . Als Stützstellen in den Teilintervallen wählen wir die arithmetischen Mittelwerte
. Als Stützstellen in den Teilintervallen wählen wir die arithmetischen Mittelwerte ![]() . Damit bilden wir die Riemann-Summen:
. Damit bilden wir die Riemann-Summen:
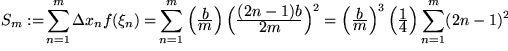
Die verbleibende letzte Summe macht etwas Mühe:
![]()
![]()
![]()
Denn die Summe der ersten ![]() Zahlen
Zahlen ![]() und die Summe der ersten
und die Summe der ersten ![]() Quadrate
Quadrate ![]() kennen wir aus Abschnitt 2.1 und
kennen wir aus Abschnitt 2.1 und ![]() . Damit erhalten wir für die Folge der Riemann-Summen:
. Damit erhalten wir für die Folge der Riemann-Summen:
und in der Grenze ![]() :
:
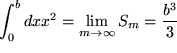
Die eigentlich noch erforderliche Überprüfung, ob das Resultat auch nicht von der Wahl der Zerlegung des Intervalls und von der Wahl der Stützstellen abhängt, schenken wir uns.
Dieses einfache Beispiel zeigt uns einerseits, dass die Definition tatsächlich zu dem erwarteten Ergebnis führt, andererseits aber auch, wieviel Mühe es schon bei einem so einfachen Beispiel kostet, nach der Definition ein derartiges Integral auszurechnen.
Wir werden uns also nach anderen Verfahren zur Berechnung von Integralen umsehen müssen, was im folgenden geschehen soll.