Als Erstes bemerken wir aufgrund unserer Kenntnisse über die Eigenschaften von Summen und die Grenzwerte von Folgen, dass das Integral linear ist, d.h. dass das Integral über eine Linearkombination von Funktionen gleich der entsprechenden Linearkombination der Integrale der einzelnen Funktionen ist: z.B. mit zwei Funktionen 
und 
und reellen Konstanten 
bzw.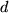 
:
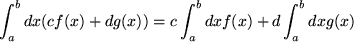
Der Spezialfall 
heißt Additivität des Intergrals:
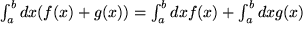
Ein anderer Spezialfall läuft unter der Bezeichnung Homogenität; wenn nämlich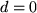 
, folgt:
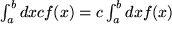
Speziell für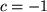 
bedeutet das:
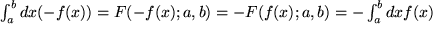
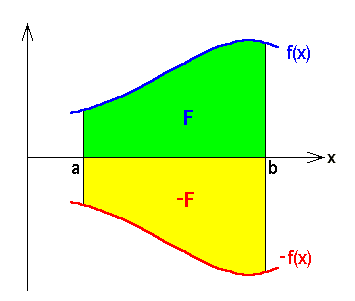
Wenn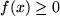 
also, wie vorausgesetzt, eine positive Funktion und 
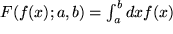der Flächeninhalt "unter" der Funktion war, erfahren wir daraus, dass das Integral über die negative, d.h. an der x-Achse gespiegelten Funktion 
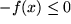genau 
ergibt, d.h. einen negativen Flächeninhalt. Der an der x-Achse gespiegelte Flächeninhalt "über" der im vierten Quadranten verlaufenden Funktion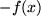 
erhält beim Integral automatisch ein negatives Vorzeichen. Wir können also getrost auf unsere anfängliche Voraussetzung 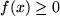verzichten, wenn wir das Integral als Flächeninhalt mit Vorzeichen deuten: positiv: "unter" einer Funktion über der x-Achse und negativ: "über" einer negativen Funktion unter der x-Achse.
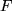und 