Mit diesen allgemeinen Kenntnissen über den Integralbegriff wollen wir uns nun der alles entscheidenden Frage der Berechnung von Riemann-Integralen zuwenden, bei der uns der Hauptsatz der Differential- und Integralrechnung, wie schon der Name verspricht, entscheidende Hilfe leistet.
Zunächst wollen wir den Riemannschen Integralbegriff erweitern: Das "bestimmte" oder Riemann-Integral 
hatte einer beschränkten stetigen Funktion 
, Integrand genannt, bei vorgegebener unterer Intervallgrenze 
und oberer Grenze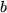 
den (mit einem Vorzeichen versehenen) Flächeninhalt 
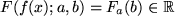unter der Funktion, also eine reelle Zahl zugeordnet. Die Mathematiker nennen so etwas ein Funktional. Nun interessiert uns, wie sich dieser Flächeninhalt ändert, wenn wir die obere Grenze verschieben. Wir ersetzen also in der oberen Grenze die Konstante 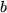durch eine Variable 
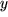und betrachten das Integral als Funktion seiner oberen Grenze. Diese Funktion von 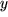heißt
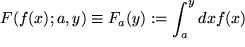
Der Vorgang ist ganz analog zu dem Erweiterungsschritt der Differentialrechnung von der Steigung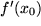 
einer Funktion an einer Stelle 
zur ersten Ableitung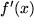 
als Funktion der Variablen 
.