Nachdem wir gelernt haben, wie man ein Integral differenziert, sind wir neugierig auf den umgekehrten Vorgang, nämlich auf das Integral über einen Differentialquotienten: Wir gehen aus von
einem Differentialquotienten 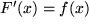 ,
der uns als stetig Funktion
,
der uns als stetig Funktion  gegeben
sei, also eigentlich von einer Differentialgleichung erster Ordnung für
gegeben
sei, also eigentlich von einer Differentialgleichung erster Ordnung für 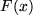 . Diesen Differentialquotienten wollen wir über das Intervall
. Diesen Differentialquotienten wollen wir über das Intervall 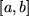 integrieren:
integrieren:
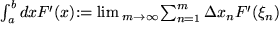
mit den Stützstellen 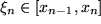 im Intervall der Länge
im Intervall der Länge 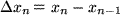 , wenn wir die Definition des Integrals einsetzen. Nach dem Mittelwertsatz der Differentialrechnung läßt sich die Steigung an der Stützstelle
, wenn wir die Definition des Integrals einsetzen. Nach dem Mittelwertsatz der Differentialrechnung läßt sich die Steigung an der Stützstelle  durch die Steigung der Sekanten, d.h. der Differentialquotient durch den Differenzenquotienten der Intervallrandpunkte ersetzen:
durch die Steigung der Sekanten, d.h. der Differentialquotient durch den Differenzenquotienten der Intervallrandpunkte ersetzen:
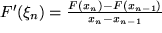
Ausgeschrieben ergibt sich dann:
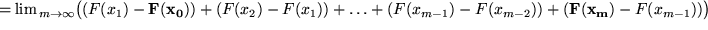
Man sieht, dass sich alle Terme paarweise wegheben bis auf den zweiten und den zweitletzten, die gar nicht mehr von 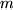 abhängen, also durch den Grenzprozeß überhaupt nicht berührt werden:
abhängen, also durch den Grenzprozeß überhaupt nicht berührt werden:
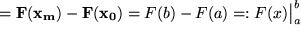 .
.
Insgesamt ergibt sich demnach als
|
Zweiter Teil des HAUPTSATZES: |
Auch in diesem Sinne ist die Integration die Umkehrung der Differentiation.
Z.B. folgt sofort wieder unser mühsam aus der Definition des Integrals hergeleitetes Ergebnis: 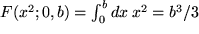 , jetzt aber mühelos aus der Differentiation
, jetzt aber mühelos aus der Differentiation 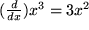 .
.
Dieser zweite Teil des Hauptsatzes ist der entscheidende Schritt zur Lösung unseres Integrationsproblems: Wir können jetzt nämlich sofort alle bestimmten Integrale berechnen von all den Funktionen, die wir in der zweiten Spalte unserer Differentiationstabelle in Kapitel 5 finden. Wir lesen die TABELLE einfach rückwärts von rechts nach links und ergänzen die Überschriften entsprechend folgendermaßen:
| TABELLE ZUR DIFFERENTIATION UND INTEGRATION | |||
| Zeile | 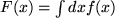 |
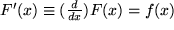 |
Bemerkungen: |
| 1 |  |
 |
|
| 2 | 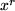 |
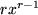 |
 |
| 3 | 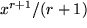 |
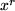 |
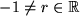 |
| 4 |  |
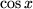 |
|
| 5 | 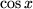 |
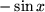 |
|
| 6 | 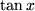 |
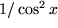 |
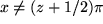 , ,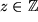 |
| 7 | 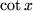 |
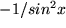 |
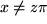 , ,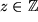 |
| 8 |  |
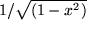 |
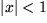 |
| 9 | 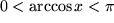 |
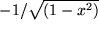 |
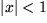 |
| 10 | 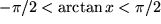 |
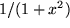 |
|
| 11 |  |
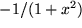 |
|
| 12 | 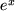 |
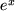 |
|
| 13 | 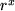 |
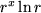 |
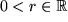 |
| 14 | 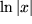 |
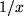 |
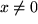 |
| 15 | 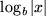 |
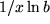 |
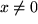 , ,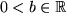 , ,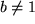 |
| 16 | 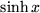 |
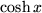 |
|
| 17 | 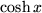 |
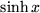 |
|
| 18 | 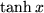 |
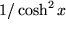 |
|
| 19 | 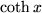 |
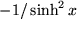 |
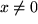 |
| 20 | 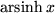 |
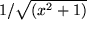 |
|
| 21 | 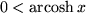 |
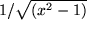 |
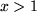 |
| 22 | 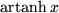 |
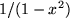 |
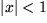 |
| 23 | 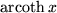 |
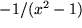 |
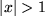 |
Unser obiges Beispiel aus der Schublade entnehmen wir z.B. der Zeile zwei für 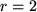 .
.
Ein weiteres Beispiel aus dieser Zeile mit den Grenzen  und
und 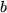 ist
ist 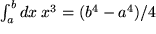 , allgemein für beliebiges reelles
, allgemein für beliebiges reelles  folgt:
folgt:
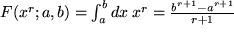 ,
,
Aus der vierten Zeile etwa finden wir:
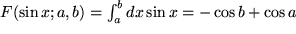 ,
,
aus der zwölften Zeile:
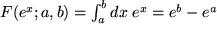 ,
,
und analog viele weitere Integrale.
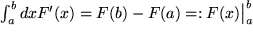 , d.h.
, d.h.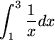
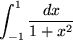
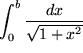
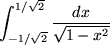

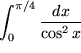
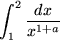
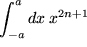 für natürliche n.
für natürliche n.