Nachdem wir nun eine beträchtliche Zahl von bestimmten Integralen über eine große Menge von Intervallen ausrechnen können, bleibt noch die Frage nach dem unbestimmten Integral eines Differentialquotienten 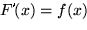 . Wir ersetzen dazu wieder die konstante obere Grenze
. Wir ersetzen dazu wieder die konstante obere Grenze 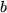 des bestimmten Integrals durch eine Variable
des bestimmten Integrals durch eine Variable 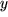 und kommen wie oben zu
und kommen wie oben zu
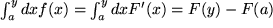
Dies schreiben wir folgendermaßen um
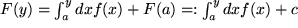 ,
,
denn  ist bezüglich der Variablen
ist bezüglich der Variablen 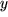 ja tatsächlich eine Konstante, die allerdings noch von dem Anfangspunkt des Intervalls
ja tatsächlich eine Konstante, die allerdings noch von dem Anfangspunkt des Intervalls  abhängt. Da man in der Funktion
abhängt. Da man in der Funktion 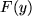 gerne wieder das übliche
gerne wieder das übliche  als Zeichen für die unabhängige Variable haben will, hat sich nun für die obige Gleichung eine unerhört schlampige Schreibweise weltweit eingebürgert: man schreibt nämlich dafür einfach symbolisch:
als Zeichen für die unabhängige Variable haben will, hat sich nun für die obige Gleichung eine unerhört schlampige Schreibweise weltweit eingebürgert: man schreibt nämlich dafür einfach symbolisch:
 und nennt
und nennt 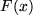 die Stammfunktion von
die Stammfunktion von 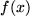 .
.
Das  auf der linken Seite dient nur als Hinweis, dass es sich um eine Funktion einer unabhängigen Variablen handelt, und hat natürlich überhaupt nichts zu tun mit der ohnehin beliebig bezeichenbaren Integrationsvariablen
auf der linken Seite dient nur als Hinweis, dass es sich um eine Funktion einer unabhängigen Variablen handelt, und hat natürlich überhaupt nichts zu tun mit der ohnehin beliebig bezeichenbaren Integrationsvariablen  auf der rechten Seite, die selbstverständlich nach der Integration rechts gar nicht mehr vorkommt. Wenn man sich diese Schlamperei einmal klargemacht hat, ist sie eine äußerst bequeme Sache und in der Tat in den größten Tafelwerken benützt und weltweit anerkannt.
auf der rechten Seite, die selbstverständlich nach der Integration rechts gar nicht mehr vorkommt. Wenn man sich diese Schlamperei einmal klargemacht hat, ist sie eine äußerst bequeme Sache und in der Tat in den größten Tafelwerken benützt und weltweit anerkannt.
So lässig geschrieben ist die Stammfunktion eigentlich eine ganze Funktionenschar mit dem Scharparameter  . Die Stammfunktion
. Die Stammfunktion 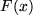 von
von  ist genau die Funktionenschar, die unsere ursprüngliche Differentialgleichung
ist genau die Funktionenschar, die unsere ursprüngliche Differentialgleichung 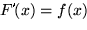 löst, und deshalb für die Physiker von so großer Wichtigkeit. Aus dieser Funktionenschar mit vorgegebenem Steigungsverlauf
löst, und deshalb für die Physiker von so großer Wichtigkeit. Aus dieser Funktionenschar mit vorgegebenem Steigungsverlauf  muß der Physiker nun nur noch durch Wahl der Konstanten
muß der Physiker nun nur noch durch Wahl der Konstanten  diejenige Lösungsfunktion aussuchen, welche die richtige Randbedingung
diejenige Lösungsfunktion aussuchen, welche die richtige Randbedingung 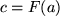 erfüllt, und schon ist das Problem gelöst.
erfüllt, und schon ist das Problem gelöst.
Gesucht ist z.B. die Stammfunktion 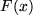 von
von 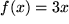 , welche die Randbedingung
, welche die Randbedingung 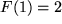 erfüllt. Aus der Funktionenschar
erfüllt. Aus der Funktionenschar 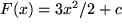 ist also diejenige Funktion auszuwählen, für die
ist also diejenige Funktion auszuwählen, für die 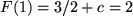 gilt, also
gilt, also 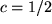 zu wählen: folglich ist
zu wählen: folglich ist 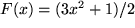 die gesuchte Lösung.
die gesuchte Lösung.
|
Aufgabe 7.2: Bestimmen Sie allgemein die Stammfunktion von folgenden Funktionen:
|
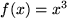
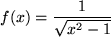
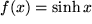
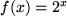
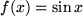 mit
mit 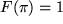
 mit
mit 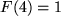
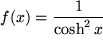 mit
mit