| Z.B. aus Zeile 14: |  . |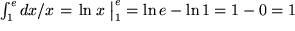
| Oder aus Zeile 4: |  . |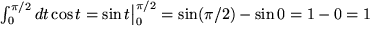
| Oder aus Zeile 10: |  . |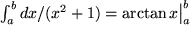
| Oder aus Zeile 8 unbestimmt: |  . |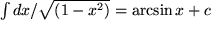
In der ersten Freude über die Konsequenzen des Hauptsatzes für die Integration durch Rückwärtslesen der Differentiationstabelle haben wir den Erfolg unserer Bemühungen etwas überschätzt. Denn bei genauerem Hinsehen sind es doch nur relativ wenige Funktionen, die in der zweiten Spalte unserer TABELLE vorkommen. Schon so einfache Funktionen unserer Grundausstattung wie etwa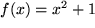 
finden wir nicht. Erst recht nicht 
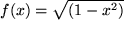, obwohl wir das Reziproke dieser Wurzel ganz einfach integrieren können. Auch bei der Gaußschen Glockenkurve 
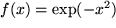sind wir mit unserer TABELLE ziemlich hilflos.
Anders als bei der Differentiation gibt es bei der Integration kein Verfahren, das automatisch bei genügendem Arbeitsaufwand zum Ziel führt. Deshalb ist Integrieren im Gegensatz zum Handwerk des Differenzierens eine Kunst.
Dennoch gibt es eine ganze Menge Regeln und Kunstkniffe, die aus den Eigenschaften des Integrals folgen und uns das Leben beträchtlich erleichtern können. Denen wollen wir uns jetzt zuwenden. Der einfachste ist die linerare Zerlegung.