Trotz aller Formeln und Tricks bleiben doch noch einige Integrale, auch in den Naturwissenschaften gebrauchte, unlösbar. Beispiele dafür sind etwa die Integranden 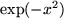 ,
, 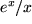 ,
, 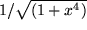 ,
, 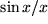 oder
oder 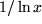 . Die Mathematiker können zwar beweisen, dass der entsprechende Grenzwert existiert, dieser läßt sich jedoch nicht in geschlossener Form durch elementare Funktionen ausdrücken.
. Die Mathematiker können zwar beweisen, dass der entsprechende Grenzwert existiert, dieser läßt sich jedoch nicht in geschlossener Form durch elementare Funktionen ausdrücken.
In dieser Lage erinnern wir uns an das unbestimmte Integral und unsere TABELLE:
| Etwa Zeile 14: | 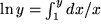 |
| oder Zeile 10: | 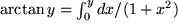 |
| oder Zeile 8: | 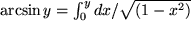 . . |
Wenn wir die Funktionen links nicht schon früher als Umkehrfunktionen kennengelernt oder als Taylor-Reihen berechnet hätten, könnte man sie sich durch diese Gleichungen definiert vorstellen.
Nach diesen Vorbildern verfährt man bei den nicht elementar darstellbaren Integralen: Man gibt einfach dem analytisch nicht lösbaren Integral einen Namen und schaut sich nach einem anderen Verfahren zur Berechnung der Funktionswerte um. Wir geben hier nur zwei Beispiele an: Die "Fehlerfunktion"
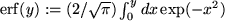 ,
,
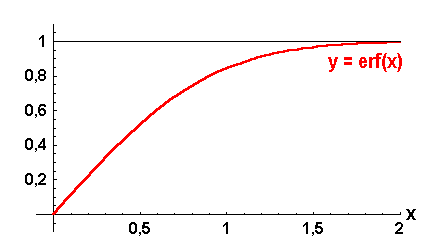
die bei der Fehlerrechnung eine Rolle spielt, und die
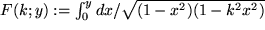 ,
,
die bei den Pendelschwingungen gebraucht werden.
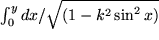 und
und 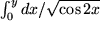 elliptische Integrale sind.
elliptische Integrale sind.