Die älteste und primitivste Art, ein bestimmtes Integral, d.h. den Flächeninhalt "unter" einer Funktion "über" einem Intervall zu berechnen, ist natürlich, den Integranden auf Millimeterpapier zu zeichnen und die Kästchen zu zählen.
Mit den elektronischen Rechnern von heute können wir das natürlich vornehmer und schneller, indem wir uns auf den definierenden Grenzwert besinnen und nach der Zerlegung des Intervalls die Flächeninhalte der Streifen aufsummieren. Dabei braucht man umso weniger Streifen bzw. Iterationsschritte je genauer man die Oberkante der Streifen der wirklichen zu integrierenden Funktion anpaßt.
Das einfachste sind dabei horizontale Geraden, wie wir das bei der Definition gemacht haben, so dass die Streifen Rechtecke werden, deren Flächeninhalt einfach zu berechnen ist. Man kann statt der Stützstellen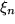 
im Inneren der Teilintervalle wie bei der Riemann-Summe, auch die Minima oder Maxima der Funktion im Teilintervall nehmen und erhält dann eine Unter- bzw. Obersumme, die in der Grenze das Integral einschließen.
Die nächst vornehmere Methode ist die Sehnen-Trapez-Regel, bei der die Funktion in jedem Teilintervall durch die Sekante approximiert und die wirklichen Flächeninhalte der Streifen durch die Trapezflächen angenähert werden. Für jedes Teilintervall nimmt man statt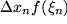 
:
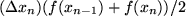
Eine noch bessere Approximation liefert die Simpson-Regel, bei der die Integrandenfunktion in den Teilintervallen jeweils durch eine Parabel nach der Keplerschen Fassregel angenähert wird. Man nimmt die Funktion also an drei Punkten in jedem Streifen:
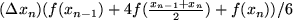
Noch raffiniertere Vorschriften zu finden, mit denen das gesuchte Integral bei vorgegebener Genauigkeitsanforderung in möglichst wenigen Schritten berechnet werden kann, ist eine der Aufgaben der numerischen Mathematik.