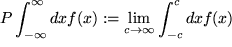
Cauchy-Hauptwert:
Es kann dabei vorkommen, dass die beiden Grenzwerte nur dann existieren, wenn die zunächst verwendeten großen endlichen Grenzen zugleich wachsen. Man nennt das Ergebnis dann den
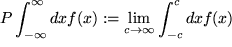
Wir berechnen dazu folgendes Beispiel für ![]() :
:
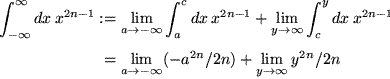
Beide Grenzwerte existieren offensichtlich nicht. Wenn wir jedoch den Hauptwert bilden, folgt:
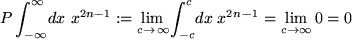
denn ein Integral einer ungeraden Funktion über ein zum Ursprung symmetrisches Intervall verschwindet.