 im Außenraum, d.h.
im Außenraum, d.h. 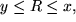 , wo das Integral lautet:
, wo das Integral lautet:Lösung:
Zunächst interessiert das von den Ladungen der Kugelschale verursachte Potential an Messpunkten  im Außenraum, d.h.
im Außenraum, d.h. 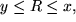 , wo das Integral lautet:
, wo das Integral lautet:
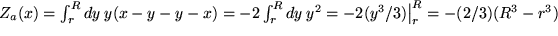 ,
,
also außer dem Coulomb-Abfall unabhängig vom Abstand  , als ob die gesamte Ladung im Mittelpunkt säße.
, als ob die gesamte Ladung im Mittelpunkt säße.
Genauso einfach finden Sie das von der Ladung der Kugelschale bewirkte Potential an Messpunkten im Abstand  vom Mittelpunkt im Innenraum der Schale, wo
vom Mittelpunkt im Innenraum der Schale, wo 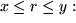 :
:
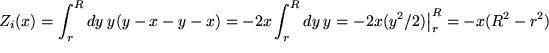 ,
,
d.h. bei Berücksichtigung des Coulomb-Faktors 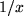 ein konstantes Potential im Inneren.
ein konstantes Potential im Inneren.
Im Schalenvolumen selbst, d.h. für 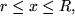 , muss das Integral in zwei Teile aufgespalten werden, da sich der Integrand ändert, wenn die Integrationsvariable
, muss das Integral in zwei Teile aufgespalten werden, da sich der Integrand ändert, wenn die Integrationsvariable 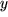 über den Messpunkt
über den Messpunkt  hinwegstreicht.
hinwegstreicht.
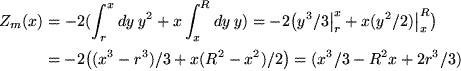
Sie können sich leicht vergewissern, dass das den stetigen Übergang des Potentials bei 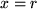 und
und 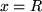 bedeutet:
bedeutet:
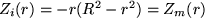
und
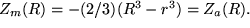
Ja Sie können sogar nachweisen, dass auch die ersten Ableitungen stetig sind, die Potentialkurve also glatt ist, d.h. keine Knicke auftreten.
Im Grenzwert  gegen
gegen 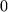 erhalten Sie das Potential innerhalb und außerhalb einer Vollkugel. Dieselbe Integration liefert Ihnen auch das Gravitationspotential z.B der Erdkugel.
erhalten Sie das Potential innerhalb und außerhalb einer Vollkugel. Dieselbe Integration liefert Ihnen auch das Gravitationspotential z.B der Erdkugel.