Wir haben in Abschnitt 2.2.4 mehr aus grundsätzlichen und mathematischen Gründen beschlossen, unseren physikalischen Überlegungen den Körper der reellen Zahlen zugrunde zu legen, obwohl die endliche Genauigkeit aller physikalischen Messungen es gestattet hätte, sich mit den rationalen Zahlen zu begnügen. In diesem Kapitel wollen wir den Zahlenraum nun noch einmal ohne zwingende physikalische Notwendigkeit erweitern, nämlich zu den komplexen Zahlen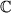 
.
Obwohl es viele mathematische Gründe gibt, den Zahlenkörper zu erweitern, so dass er auch die Lösung der Gleichung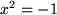 
enthält, und bei dieser Erweiterung außerdem auch viele unerwartete und tiefe Einsichten möglich wurden, sind die komplexen Zahlen für die Physik nur ein typisches Hilfsmittel. An keiner Stelle der Physik ist es wirklich notwendig, die komplexen Zahlen zu verwenden. Dennoch sind sie in weiten Bereichen eine äußerst bequeme Art der Darstellung für viele Phänomene. Sie können sich noch gar nicht vorstellen, wie bequem etwas Überflüssiges sein kann! Nicht nur bei allen Schwingungsvorgängen und in der Elektrotechnik gehören die komplexen Zahlen zum täglichen Werkzeug, sondern vor allem die Quantenmechanik enthält ganz wesentlich komplexe Größen, ja der entscheidende Unterschied der Schrödinger-Gleichung etwa zur Wärmeleitungsgleichung ist die imaginäre Einheit "
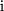". Ohne Verwendung der komplexen Zahlen müßte man statt einer einfachen komplexen Gleichung zwei kompliziert gekoppelte reelle Differentialgleichungen behandeln und lösen lernen. Deshalb ist dieses Kapitel auch eine direkte Vorbereitung auf Ihre Quantenmechanik-Vorlesung.
Die überraschenden Ergebnisse der komplexen Zahlen für die Mathematik sind auch für sich allein schon interessant und einige Mühe wert: Mit der Erweiterung von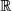 
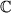auf wird nicht nur 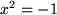, sondern jede Gleichung zweiten Grades lösbar, ja sogar jede algebraische Gleichung 
-ten Grades hat nach dem Fundamentalsatz der Algebra genau Lösungen in 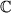. Jede rationale Funktion hat eine Partialbruchzerlegung. Erst jetzt wird der Konvergenzradius der Potenzreihen verständlich aus dem Definitionsbereich und vieles andere mehr.
So ergibt sich die Frage: Was muss getan werden, um in dieses Paradies zu gelangen?