Mit den reellen Zahlen ist, wie wir gesehen haben, zwar jede Gleichung
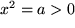lösbar:
,
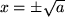aber es existiert keine reelle Zahl
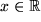, für die
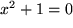ist.
Wir sehen das indirekt: Gäbe es nämlich eine solche reelle Zahl
,
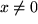dann müßte für diese Zahl auf der reellen Zahlengeraden entwe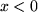der
oder
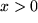sein,
also die Quadratzahl
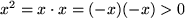sein.
Folglich müßte auch
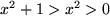sein,
und das wäre ein Widerspruch zu unserer Ausgangsgleichung:
.
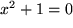Die Erweiterung der reellen Zahlen erfordert also wenigstens die Hinzunahme der Lösung
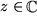der Gleichung
.
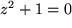Dieses Problem wurde 1777 von Euler mit einem genialen Trick dadurch gelöst,
dass er der unbekannten neuen Zahl einfach einen Namen gab:
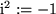
Damit kann man die Lösung der Gleichung
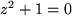einfach hinschreiben:
.
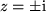Zunächst ziehen wir einige direkte Folgerungen aus dieser Definition für die Potenzen von
,
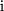wobei wir versuchen alle vom Körper der reellen Zahlen her bekannten Rechenregeln
einfach beizubehalten:
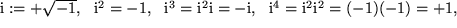usw.
|
|
.Auch die negativen Potenzen erhalten wir leicht: Zunächst folgt für die zu
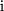inverse Zahl
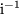aus
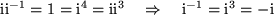
und weiter:
,
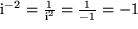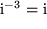, usw.
D.h. die oben eingerahmten Ergebnisse gelten sogar für alle ganzen Zahlen
.
|
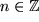Aufgabe 8.1: Berechnen Sie:
|
,
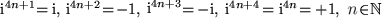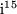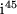und
.
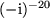