Mit diesem ersten Erfolg gehen wir sogleich an die allgemeinere Gleichung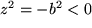 
und finden als Lösung 
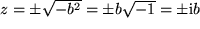. Wir nennen eine mit der imaginären Einheit 
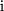multiplizierte reelle Zahl eine
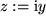mit 
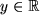
Wenn wir noch allgemeinere Gleichungen betrachten, nämlich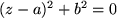 
, erhalten wir als Lösung 
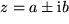, also eine Linearkombination einer reellen und einer imaginären Zahl. Dies nennen wir eine allgemeine
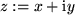mit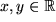 
Eine komplexe Zahl ist also ein geordnetes Paar eindeutig festgelegter reeller Zahlen: der rein reelle erste Teil heißt
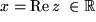
und der mit dem Faktor 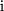versehene zweite Teil heißt
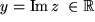
Diese Zerlegung in Real- und Imaginärteil ist eindeutig im Gegensatz zu den rationalen Zahlen, die wir ebenfalls als "geordnete Paare" damals von ganzen Zahlen eingeführt hatten, bei denen wir aber ganze Äquivalenzklassen identifiziert haben: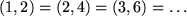 
denn das "Kürzen" sollte möglich sein, ohne die Zahl zu ändern: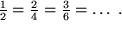 
Die Gleichheit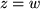 
zweier komplexer Zahlen 
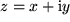und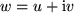 
bedeutet die Gleichheit der beiden Real- und der Imaginärteile: 
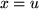und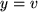 
, d.h.
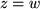beinhaltet zwei reelle Gleichungen 
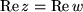und 
.
Speziell verschwindet eine komplexe Zahl nur genau dann, wenn Real- und Imaginärteil beide gleich Null si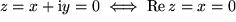nd:
und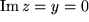 
.
Die reellen Zahlen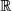 
: sind eine Teilmenge der Menge der komplexen Zahlen: 
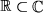, nämlich alle diejenigen mit 
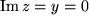. Dazu kommen die rein imaginären Zahlen 
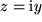als neue Elemente hinzu.
Bevor wir uns den Rechenregeln zuwenden, wollen wir einen Überblick gewinnen über die Methoden, die komplexen Zahlen zu veranschaulichen: