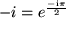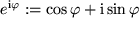Wenn wir in die Darstellung der komplexen Zahlen in ebenen Polarkoordinaten für Cosinus und Sinus die Taylor-Entwicklungen einsetzen, stoßen wir auf eine interessante Relation:
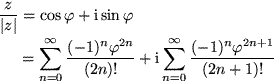
Falls wir darin die Relation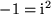 
berücksichtigen, erhalten wir:
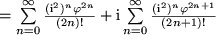und zusammengezogen:
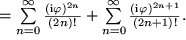Ausgeschrieben ergibt das: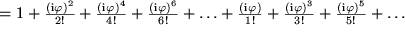
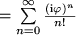
Diese Reihe kommt uns bekannt vor. Wir erkennen darin die Taylor-Reihe, die es uns gestattet hat, die Funktionswerte der Exponentialfunktion zu berechnen, nur dass da jetzt vor der reellen Variablen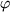 
ein 
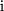steht. Dadurch fühlen wir uns ermutigt, durch die obige Reihe die Exponentialfunktion für eine imaginäre Variable zu definieren:
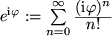
Mit dieser Definition erhält die gefundene Relation eine ganz einfache Gestalt, sie ist berühmt unter dem Namen:
|
Euler-Formel: |
Daraus entnehmen wir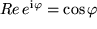 
und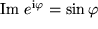 
. Da Cosinus und Sinus periodische Funktionen mit der Periode 
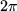sind, muß demnach auch die Exponentialfunktion einer imaginären Variablen eine 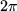-periodische Funktion sein:
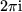-periodisch: 
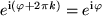mit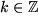 
Mit der Euler-Formel haben wir neben den Darstellungen der komplexen Zahlen in kartesischen und Polarkoordinaten eine dritte sehr beliebte Darstellung erhalten:
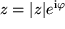
Speziell für folgende komplexe Zahlen auf dem Einheitskreis: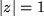 
stellen wir zum Auswendiglernen einige wichtige Relationen zusammen:
, 
, 
, 
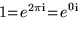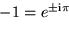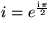