Auch bei der Multiplikation regelt Eulers 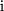 alles automatisch. Wir können mit den von den reellen Zahlen gewohnten Gesetzen die beiden komplexen Zahlen
alles automatisch. Wir können mit den von den reellen Zahlen gewohnten Gesetzen die beiden komplexen Zahlen 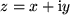 und
und 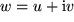 einfach miteinander multiplizieren und
einfach miteinander multiplizieren und 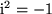 berücksichtigen:
berücksichtigen:
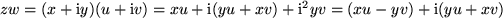
So erhalten wir einen ziemlich komplizierten Ausdruck für das
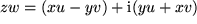
Dieser Ausdruck läßt sich nicht leicht im kartesischen Koodinatensystem veranschaulichen, auch wenn wir ihn mit 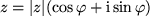 bzw.
bzw. 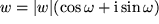 in Polarkoordinaten umschreiben:
in Polarkoordinaten umschreiben:
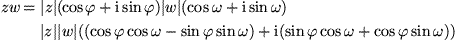
Deshalb gehen wir mit der Eulerschen Formel 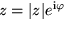 und
und 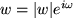 zur Exponentialdarstellung über, die unserem Wunsch nach Veranschaulichung entgegenkommt:
zur Exponentialdarstellung über, die unserem Wunsch nach Veranschaulichung entgegenkommt:
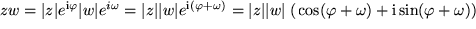
Das bedeutet für den
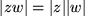
und für das
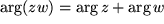
Aus der Gleichung für die Beträge entnehmen wir, dass 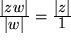 , d.h. dass sich die Länge
, d.h. dass sich die Länge 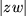 des Produktzeigers zur Länge
des Produktzeigers zur Länge 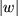 des Zeigers des einen Faktors verhält wie die Länge
des Zeigers des einen Faktors verhält wie die Länge  des Zeigers des anderen Faktors zu
des Zeigers des anderen Faktors zu 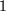 . Zur Veranschaulichung haben wir also von dem einen Faktorzeiger, z.B.
. Zur Veranschaulichung haben wir also von dem einen Faktorzeiger, z.B. 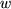 aus das Argument
aus das Argument 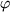 des anderen Faktors anzutragen, um genau dann den Produktzeiger
des anderen Faktors anzutragen, um genau dann den Produktzeiger 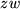 zu erhalten, wenn das Dreieck
zu erhalten, wenn das Dreieck 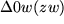 dem Dreieck
dem Dreieck 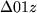 ähnlich ist. Wir illustrieren dies im nächsten Bild:
ähnlich ist. Wir illustrieren dies im nächsten Bild:
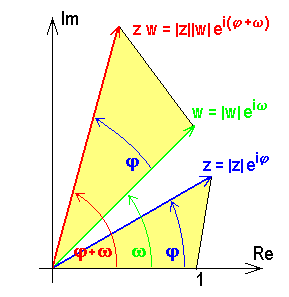
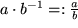 löst die Gleichung
löst die Gleichung 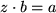 für
für 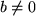 . Zur Veranschaulichung des Quotienten berechnen wir
. Zur Veranschaulichung des Quotienten berechnen wir
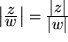
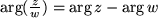
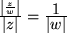 , d.h. die Länge
, d.h. die Länge 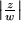 des Quotientenzeigers verhält sich zur Länge
des Quotientenzeigers verhält sich zur Länge 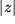 des Zeigers des Zählers wie 1 zur Länge
des Zeigers des Zählers wie 1 zur Länge  des Nenners. Zur Veranschaulichung haben wir also vom Argument
des Nenners. Zur Veranschaulichung haben wir also vom Argument  aus das Argument
aus das Argument 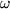 des Nenners abzuziehen, um genau dann den Quotientenzeiger
des Nenners abzuziehen, um genau dann den Quotientenzeiger 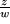 zu erhalten, wenn das Dreieck
zu erhalten, wenn das Dreieck 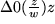 dem Dreieck
dem Dreieck 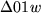 ähnlich ist. Wir sehen uns das wieder genauer im nächsten Bild an:
ähnlich ist. Wir sehen uns das wieder genauer im nächsten Bild an: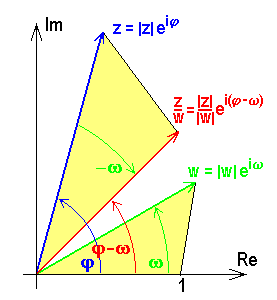
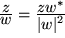 ,
,
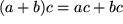
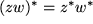
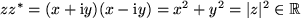
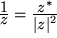 .
.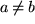 und
und 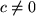 folgt
folgt 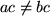 .
.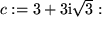 :
: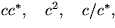
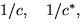
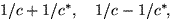
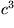
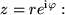 :
: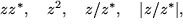
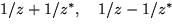
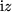
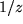
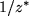 .
.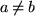 ,
,  nicht gelten würde, wenn wir statt der durch Eulers
nicht gelten würde, wenn wir statt der durch Eulers 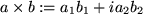 gewählt hätten.
gewählt hätten.