Auch die Übertragung des für die reellen Folgen und Funktionen zentralen Begriff des Grenzwerts bereitet uns keine ernsten Probleme, da es dabei auf den Abstand zwischen Punkten ankam, den wir auch im Komplexen zur Verfügung haben.
Wir sagen, eine Folge von komplexen Zahlen 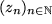 hat eine komplexe Zahl
hat eine komplexe Zahl 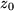 als Grenzwert oder Limes und schreiben:
als Grenzwert oder Limes und schreiben: 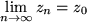 ( manchmal lässiger:
( manchmal lässiger: 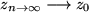 ), oder nennen die Folge:
), oder nennen die Folge:
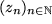 konvergent gegen
konvergent gegen 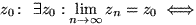 :
: 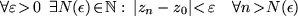
Mit dem letzten Stenogramm ist wieder gemeint: für jede vorgegebene auch noch so kleine positive Zahl  kann man eine Nummer
kann man eine Nummer 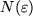 angeben, so dass der Abstand vom Häufungspunkt
angeben, so dass der Abstand vom Häufungspunkt 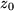 für alle Folgenglieder mit einer größeren Nummer als
für alle Folgenglieder mit einer größeren Nummer als 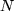 kleiner ist als das vorgegebene kleine
kleiner ist als das vorgegebene kleine  .
.
Mit dieser Definition des Grenzwerts komplexer Zahlen sind alle Konvergenzbetrachtungen im Komplexen auf die Untersuchung der entsprechenden reellen Abstände zurückgeführt.
Für die komplexen Funktionen wählen wir wieder eine Folge 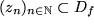 von komplexen Zahlen im Definitionsbereich
von komplexen Zahlen im Definitionsbereich 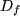 der Funktion
der Funktion 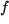 , die für
, die für 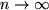 gegen die Zahl
gegen die Zahl 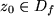 strebt. Dann bilden wir die Funktionswerte an diesen Stellen
strebt. Dann bilden wir die Funktionswerte an diesen Stellen 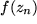 , die wieder eine Folge darstellen
, die wieder eine Folge darstellen 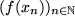 , und überprüfen, ob diese Folge der Funktionswerte konvergiert. Falls sich das für jede aus dem Definitionsbereich herausgegriffene gegen
, und überprüfen, ob diese Folge der Funktionswerte konvergiert. Falls sich das für jede aus dem Definitionsbereich herausgegriffene gegen 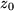 strebende Folge zeigen läßt und denselben Grenzwert
strebende Folge zeigen läßt und denselben Grenzwert 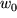 ergibt, nennen wir die Folge der Funktionswerte konvergent gegen
ergibt, nennen wir die Folge der Funktionswerte konvergent gegen 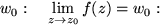
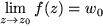 konvergent:
konvergent: 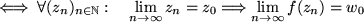
Wenn wir unsere Definition der Konvergenz für Folgen einsetzen, ergibt das:
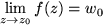 konvergent:
konvergent: 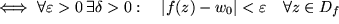 mit
mit 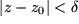
Dies für alle Folgen zu zeigen, ist natürlich wieder leichter gesagt als getan! Wir überlassen dieses Problem wie schon früher im Reellen den Mathematikern und beschränken uns auf die uns interessierenden meist ohnehin klaren Fälle.
Mit dieser Grenzwertdefinition können wir leicht auch für unsere komplexen Funktionen die Stetigkeit definieren analog unserer früheren Definition:
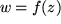 stetig bei
stetig bei 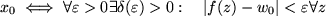 mit
mit 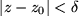
Für die Grenzwerte bedeutet das wieder, dass an der betrachteten Stelle 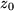 der Limes durch den Funktionswert
der Limes durch den Funktionswert 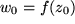 des Grenzwerts
des Grenzwerts 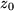 einer Folge
einer Folge 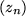 aus dem Definitionsbereich der Argumente gegeben wird:
aus dem Definitionsbereich der Argumente gegeben wird: 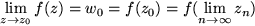 . Anschaulich heißt das, dass die Funktion
. Anschaulich heißt das, dass die Funktion 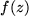 dem Punkt
dem Punkt 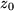 benachbarte Punkte wieder in benachbarte Bildpunkte abbildet.
benachbarte Punkte wieder in benachbarte Bildpunkte abbildet.