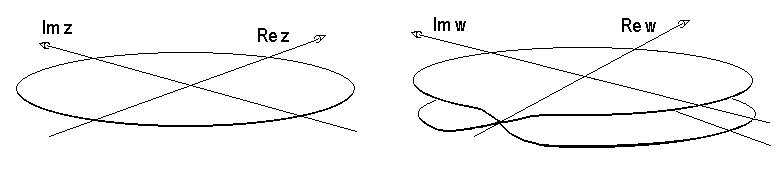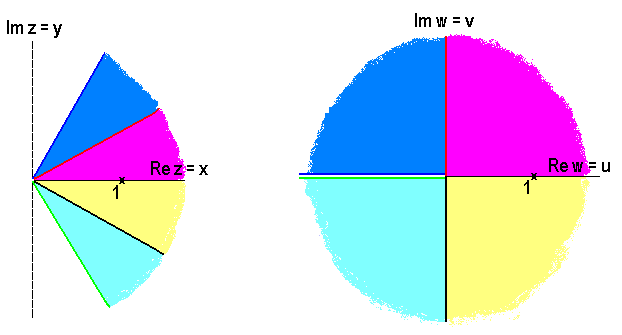8 Komplexe Zahlen
8.3 Funktionen einer komplexen Variablen
8.3.4 Potenzen
Zunächst betrachten wir wie früher die Potenzen 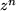 mit natürlichen Exponenten
mit natürlichen Exponenten 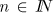 :
:
wobei wir zum Schluß die Euler-Formel verwendet und so deren Erweiterung erhalten haben: die
|
Moivre-Formel: 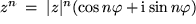
|
Das bedeutet für den
Betrag der n-ten Potenz:
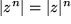
.
und für das
Argument der n-ten Potenz:
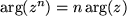
.
Wir wollen zwei Beispiele genauer diskutieren:
1) Als erstes Beispiel wählen wir die Quadrat-Funktion, d.h. 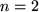 :
:
Quadrat-Funktion:
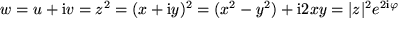
.
d.h. für den Realteil: 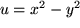 und den Imaginärteil:
und den Imaginärteil: 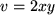
bzw. für den Betrag: 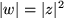 und für das Argument:
und für das Argument: 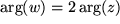 .
.
Zunächst berechnen wir einige Bildpunkte:
Dann betrachten wir die senkrechte Gerade 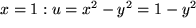 und
und 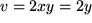 . Daraus folgt
. Daraus folgt 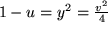 , also
, also 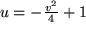 , d.h. die Gleichung einer nach links offenen Parabel.
, d.h. die Gleichung einer nach links offenen Parabel.
Analog zeigt man, dass die waagrechte Gerade 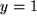 in die nach rechts offene Parabel
in die nach rechts offene Parabel 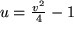 übergeht.
übergeht.
Der Einheitskreis 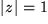 geht offenbar bei der Quadrat-Abbildung in sich über:
geht offenbar bei der Quadrat-Abbildung in sich über: 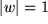 .
.
Aus  sieht man, dass die Hyperbeln mit den Winkelhalbierenden als Asymptoten in senkrechte Geraden und aus
sieht man, dass die Hyperbeln mit den Winkelhalbierenden als Asymptoten in senkrechte Geraden und aus 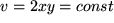 , dass die Hyperbeln mit den Achsen als Asymptoten in waagrechte Geraden übergehen.
, dass die Hyperbeln mit den Achsen als Asymptoten in waagrechte Geraden übergehen.
Das folgende Bild vermittelt einen Überblick über die gesamte Abbildung. Dabei ist bei der Urbild-Ebene die linke Hälfte weggelassen, da das Bild der rechten Hälfte allein schon die ganze w-Ebene überdeckt.
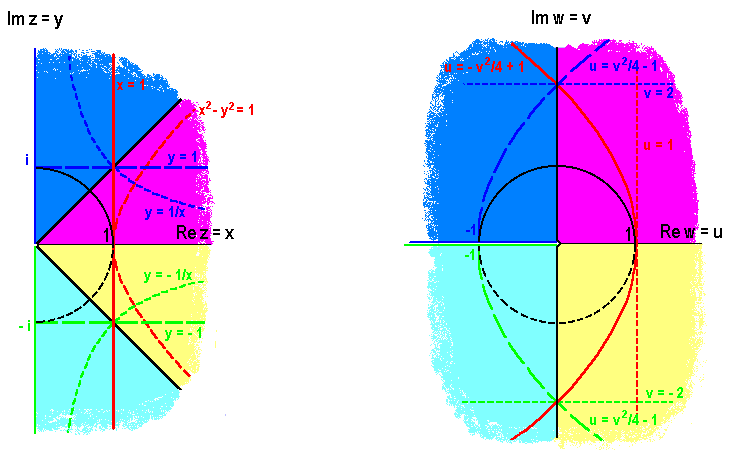
Bild 8.9: Rechte Hälfte der z- und gesamte obere w-Ebene der Quadrat-Funktion
Man kann sich die Abbildung etwa folgendermaßen zustandegekommen vorstellen: man denke sich
die z-Ebene aus Gummifolie bestehend und klappe die positive und die negative imaginäre Halbachse
um den Ursprung um
 nach links in die negative reelle Achse, bis sie sich treffen.
nach links in die negative reelle Achse, bis sie sich treffen.
Die Bilder der linken Hälfte der Gaußschen z-Ebene ergeben eine zweite Überdeckung
der ganzen w-Ebene, ähnlich wie auch schon bei der reellen Quadrat-Funktion das Bild der
negativen Urbild-Halbgeraden die positive Bild-Halbgerade ein zweites Mal überdeckte, weshalb
die Wurzel-Funktion nur über der positiven Halbgerade definiert werden konnte. Um hier bei der
komplexen Quadrat-Funktion eine Umkehrfunktion über der ganzen Ebene zu ermöglichen,
schneiden die Mathematiker die beiden übereinander liegend gedachten Bild-Ebenen (z.B. entlang der
negativen reellen Achse) auf und verbinden das obere Ufer des Schnittes im oberen Blatt mit dem
unteren Ufer im unteren Blatt und denken sich auch das untere Ufer des oberen Blattes "durch die
andere Verbindung hindurch" mit dem oberen Ufer des unteren Blattes verklebt. Das ganze Gebilde
aus den zwei kreuzweise entlang der negativen reellen Achse verbundenen Ebenen nennt man eine
Riemannsche Fläche mit zwei Blättern, so dass man sagen kann: die komplexe Quadrat-Funktion
bildet die z-Ebene umkehrbar eindeutig auf eine zweiblättrige Riemannsche Fläche ab, wobei die
spezielle Lage des Schnittes willkürlich ist; entscheidend ist nur, dass er zwischen den beiden
Verzweigungspunkten
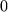 und
und 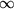 verläuft. Die nächste Abbildung versucht diesen Sachverhalt anschaulich darzustellen.
verläuft. Die nächste Abbildung versucht diesen Sachverhalt anschaulich darzustellen.
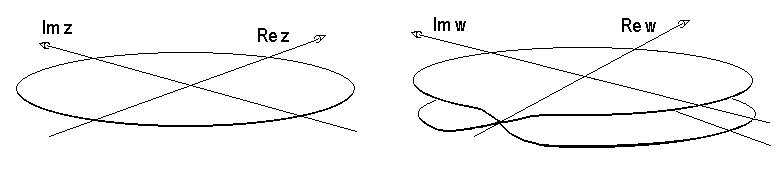
Bild 8.10: Riemannfläche der Quadrat-Funktion
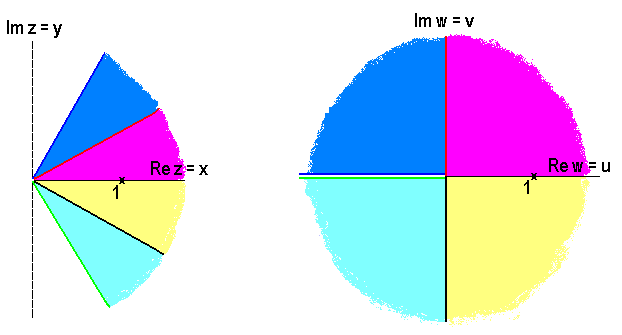
Bild 8.11: Ein Drittel der z-Ebene und oberes Blatt der w-Ebene für 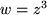
![]() mit natürlichen Exponenten
mit natürlichen Exponenten ![]() :
:![]() :
:![]() und den Imaginärteil:
und den Imaginärteil: ![]()
![]() und für das Argument:
und für das Argument: ![]() .
.![]() und
und ![]() . Daraus folgt
. Daraus folgt ![]() , also
, also ![]() , d.h. die Gleichung einer nach links offenen Parabel.
, d.h. die Gleichung einer nach links offenen Parabel.![]() in die nach rechts offene Parabel
in die nach rechts offene Parabel ![]() übergeht.
übergeht.![]() geht offenbar bei der Quadrat-Abbildung in sich über:
geht offenbar bei der Quadrat-Abbildung in sich über: ![]() .
.![]() sieht man, dass die Hyperbeln mit den Winkelhalbierenden als Asymptoten in senkrechte Geraden und aus
sieht man, dass die Hyperbeln mit den Winkelhalbierenden als Asymptoten in senkrechte Geraden und aus ![]() , dass die Hyperbeln mit den Achsen als Asymptoten in waagrechte Geraden übergehen.
, dass die Hyperbeln mit den Achsen als Asymptoten in waagrechte Geraden übergehen.