Die bei weitem wichtigste komplexe Funktion ist die natürliche Exponentialfunktion. Wir wurden bereits im Abschnitt 8.1.5 durch die Euler-Formel auf ihre Definition für rein imaginäre Variable geführt und können diese natürlich leicht für allgemeine komplexe Variablen ergänzen:
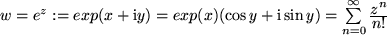
d.h. für den Betrag: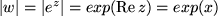 
und für das Argument: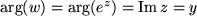 
.
Während sie als Funktion des Realteils nach wie vor so rasant ansteigt, wie wir früher gesehen hatten, ist sie in Abhängigkeit vom Imaginärteil ihrer Variablen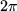 
-periodisch.
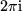-periodisch: 
mit 
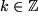
Der Konvergenzradius der Taylor-Entwicklung ist, wie wir früher gesehen haben, unendlich.
für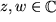 
gilt nach wie vor.
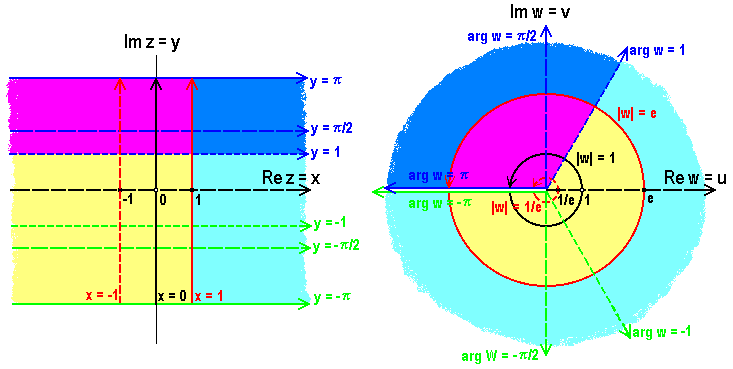
Um uns ein Bild der Funktion machen zu können, berechnen wir zunächst wieder einige Bildpunkte:
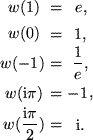
Dann sehen wir, dass die senkrechten Geraden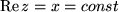 
in Kreise 
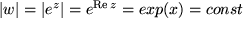übergehen: die Gerade 
in den mit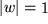 
, die mit 
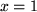in den 
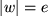und die Gerade 
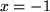in den Kreis mit 
.
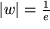Die waagrechten Geraden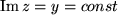 
werden in Speichen 
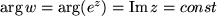abgebildet, und zwar die Gerade 
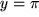in die Speiche 
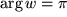, die Gerade 
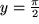in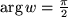 
, usw..
Aus diesen Ergebnissen erkennen wir, dass die Exponentialfunktion einen waagrechten Streifen der z-Ebene mit der Höhe 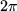, z.B. den sogenannten Fundamentalbereich mit 
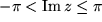auf die zwischen den Verzweigungspunkten 
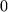und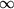 
(z.B. entlang der negativen reellen Achse) aufgeschnittene w-Ebene abbildet. Die ganze z-Ebene geht also in eine Riemann-Fläche mit unendlich vielen Blättern über. Bei jedem Blatt ist dabei das obere Ufer entlang dem Schnitt mit dem unteren Ufer des darunterliegenden Blattes stetig verbunden und das obere Ufer des letzten "durch alle anderen Verbindungen hindurch" mit dem unteren Ufer des ersten Blattes. Die folgende Darstellung kann helfen, sich ein Bild von dem Wirken der Funktion zu machen.
