8 Komplexe Zahlen
8.3 Funktionen einer komplexen Variablen
8.3.6 Trigonometrische Funktionen
Nachdem wir die Exponentialfunktion untersucht haben, werfen wir noch einen kurzen Blick auf die trigonometrischen Funktionen, Cosinus und Sinus, die wir mit Hilfe der Euler-Formel leicht aus der Exponentialfunktion erhalten oder durch ihre Potenzreihen definieren können:
Cosinus:

und
Sinus:
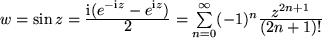
.
Beide Reihen konvergieren in der ganzen Ebene. Wie wir wissen, sind Cosinus und Sinus
Ebenso wie unsere alten trigonometrischen Additionstheoreme aus Abschnitt 4.2.2: :
gelten auch 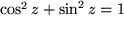 ,
, 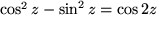 und
und 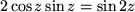 für allgemeine komplexe Variable
für allgemeine komplexe Variable 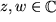 :
:
Speziell für 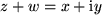 erhält man daraus mit
erhält man daraus mit
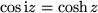
bzw.
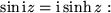
:
Dabei sind die Hyperbel-Funktionen definiert wie früher:
cosinus hyperbolicus:
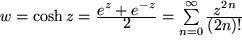
und
sinus hyperbolicus:
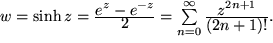
.
Man sieht daraus, dass 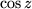 und
und 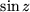 im Komplexen keineswegs mehr beschränkt sind, sondern für große Imaginärteile ansteigen wie die
Hyperbel-Funktionen.
im Komplexen keineswegs mehr beschränkt sind, sondern für große Imaginärteile ansteigen wie die
Hyperbel-Funktionen.
Anders als bei der Exponentialfunktion werden hier senkrechte Streifen der z-Ebene mit der Breite 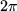 , z.B. der Fundamentalbereich mit
, z.B. der Fundamentalbereich mit 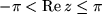 , auf die zwischen
, auf die zwischen 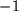 und
und 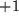 aufgeschnittene zweiblättrige w-Ebene abgebildet.
aufgeschnittene zweiblättrige w-Ebene abgebildet.
|
Aufgabe 8.9: Additionstheoreme
Beweisen Sie eines der Additionstheoreme, etwa 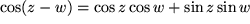 , mit Hilfe der Exponentialfunktionen und dann daraus , mit Hilfe der Exponentialfunktionen und dann daraus 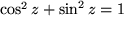 . Lösung . Lösung
|
|
Aufgabe 8.10: Zusammenhang mit den hyperbolischen Funktionen
Zeigen Sie, dass:
|
An der komplexen Sinus-Funktion wollen wir die Vielfalt der Darstellungsmöglichkeiten demonstrieren, die uns zur Verfügung stehen. Wegen der Symmetrieeigenschaften genügt es, 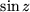 über dem Quadrat
über dem Quadrat 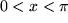 und
und 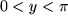 zu betrachten:
zu betrachten:
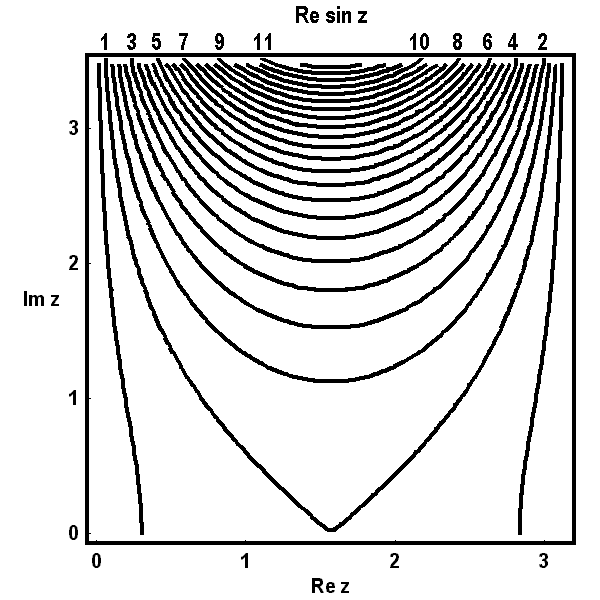
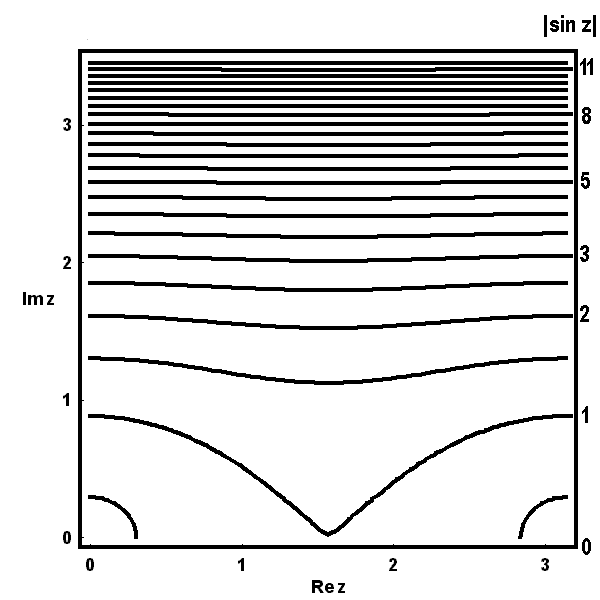
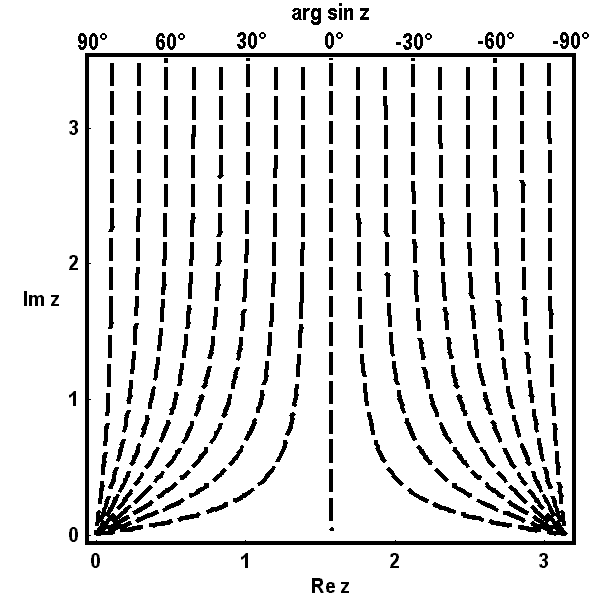
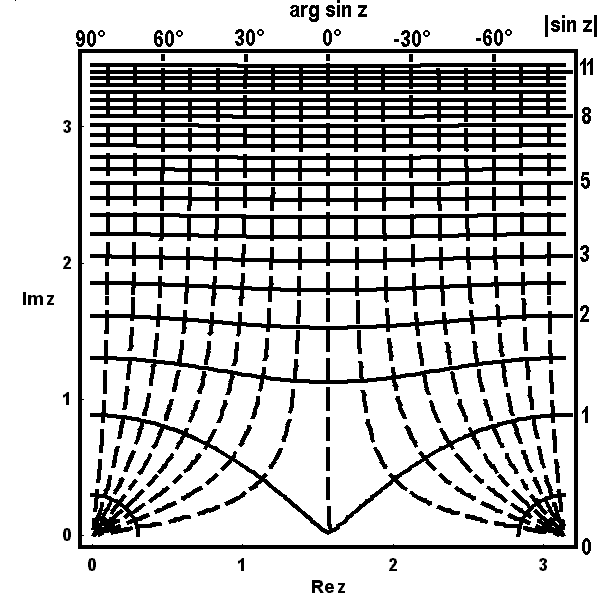
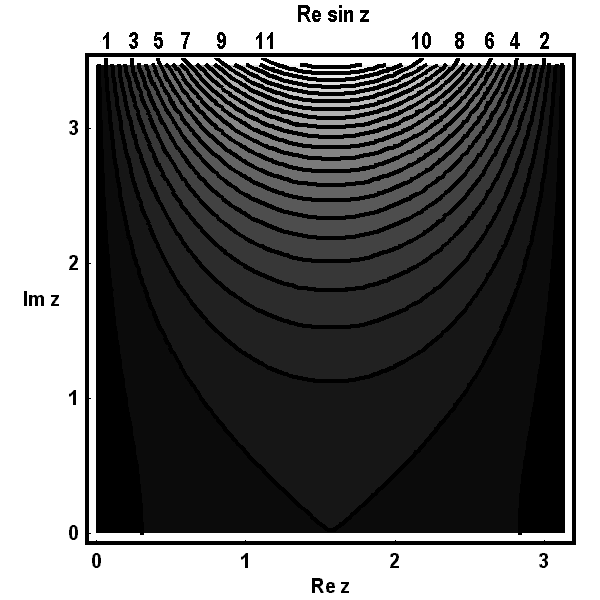
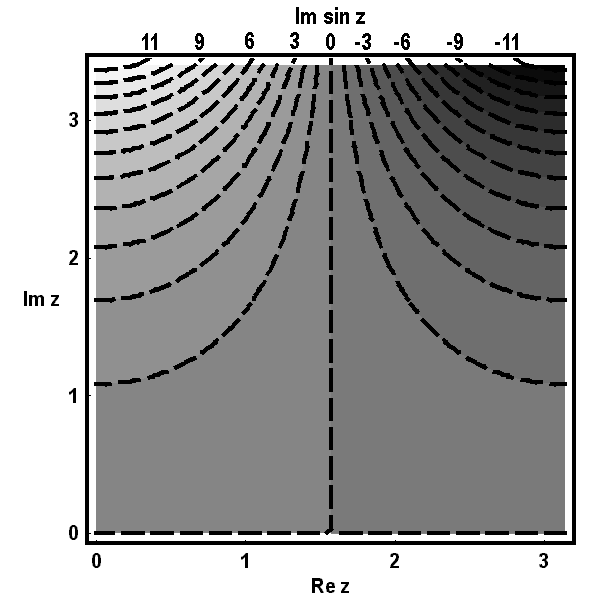
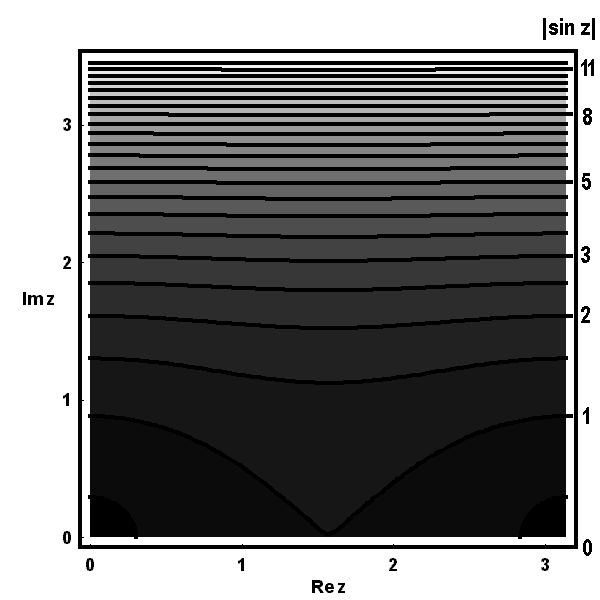
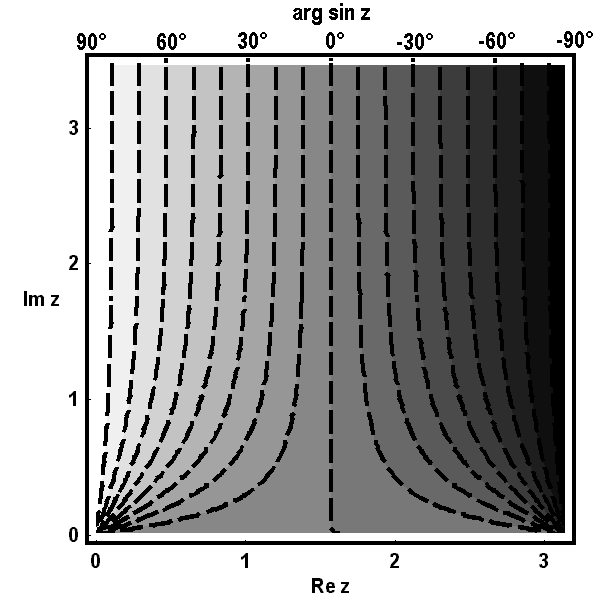
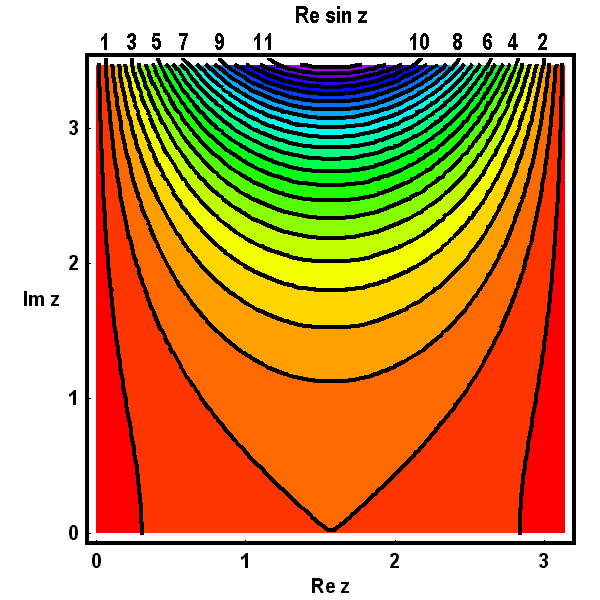
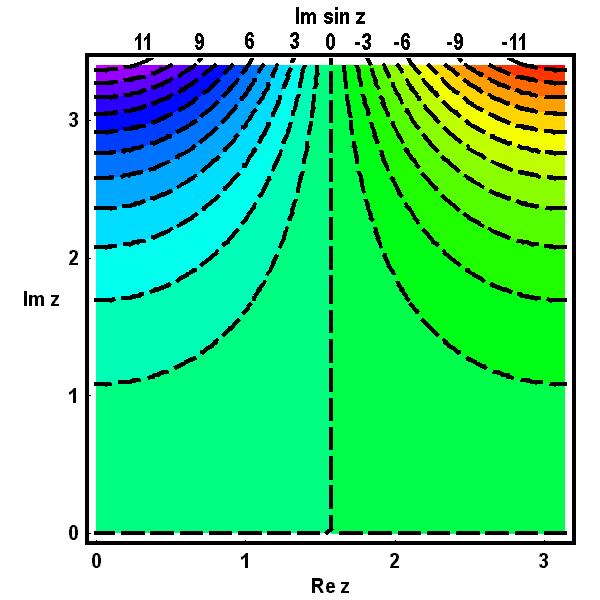
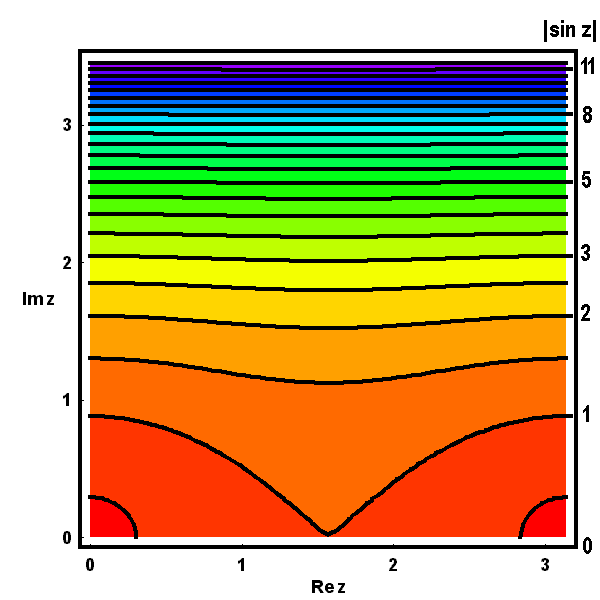
Die folgenden Bilder zeigen zunächst die Höhenlinien für Realteil  , Imaginärteil
, Imaginärteil 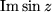 (gestrichelt), Betrag
(gestrichelt), Betrag 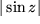 und Argument
und Argument 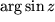 (ebenfalls gestrichelt) der Bildfunktion
(ebenfalls gestrichelt) der Bildfunktion 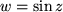 über dem Quadrat.
über dem Quadrat.
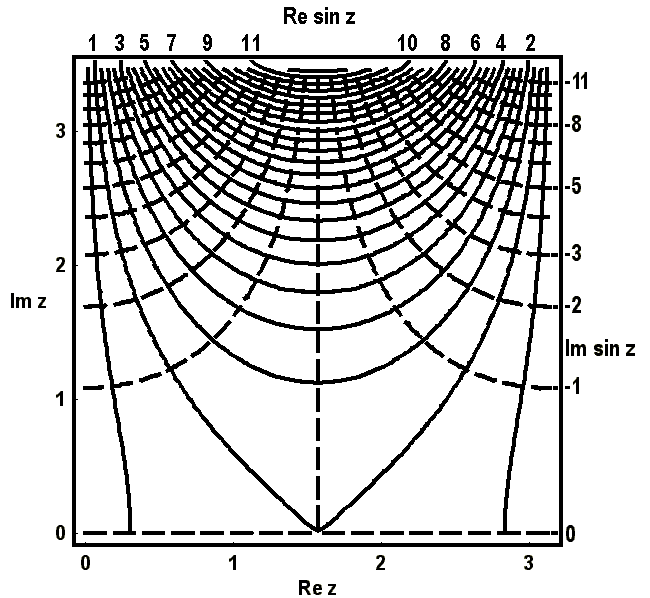
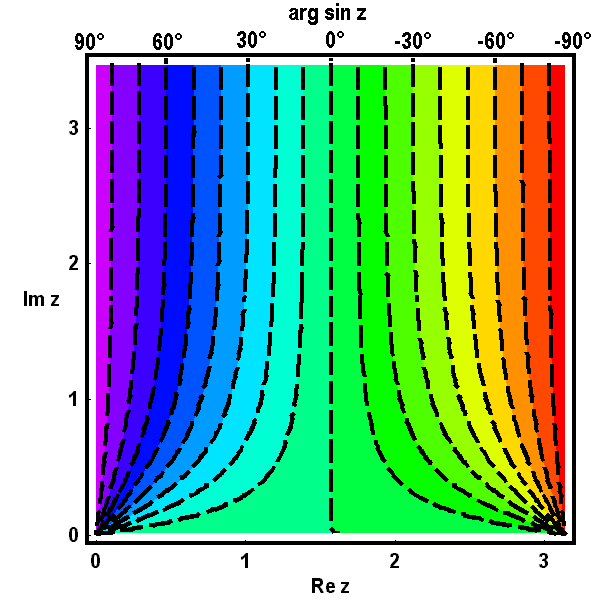
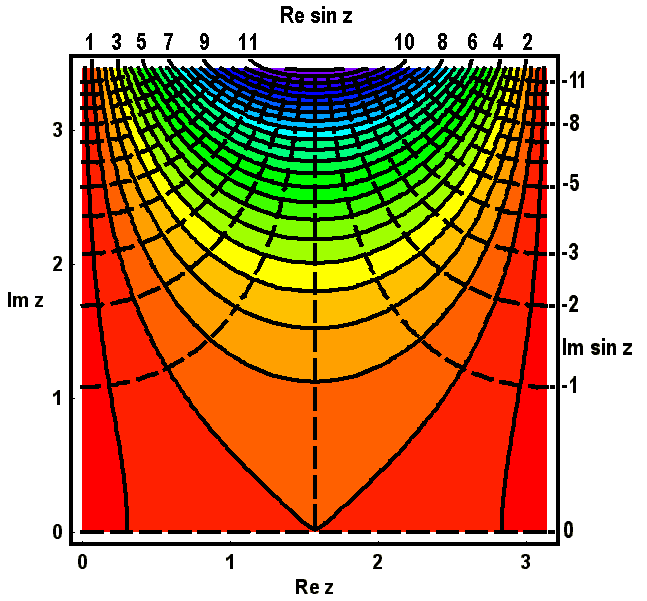
Üblicherweise faßt man diese paarweise in einem Diagramm zu einem Höhenliniennetz zusammen, wie in den nächsten beiden Bildern geschehen:
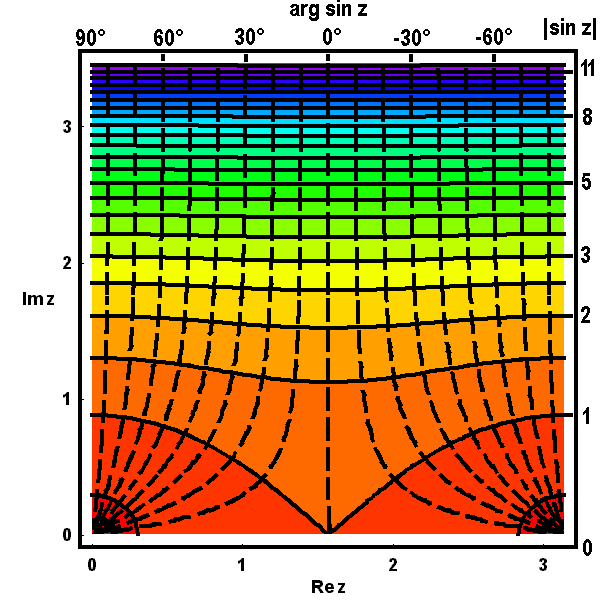
Noch schönere einprägsame Bilder erhält man, wenn man zur Charakterisierung der relativen Höhen eine Farbskala verwendet, etwa wie in geographischen Karten vom Dunkelblau der Meerestiefen über verschiedene Grüntöne bis zum immer dunkler werdenden Braun der Gebirge oder wie in dem hier bei den Bildern k) bis n) verwendeten Computer-Programm MATHEMATICA die Farben des Regenbogens entsprechend der Frequenz des Lichtes von (magma-)roten Tönen für kleinere Werte bis (himmel-)blauen bei hohen Funktionswerten anwachsend. Diese Bilder vermitteln einen deutlichen Eindruck von der Struktur des betrachteten "Gebirges der Funktionswerte".
Auch bei dieser Darstellungsart können wieder die farblich veranschaulichten Höhenlinien einer Variablen zu einem Netz ergänzt werden durch Eintragen der (gestrichelten) Höhenlinien einer zweiten Variablen, die allerdings dann nicht mehr farblich kommentiert werden können. Das wird in den nächsten beiden Bildern illustriert:
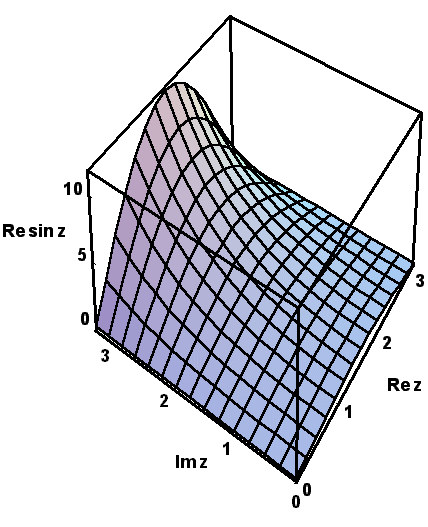
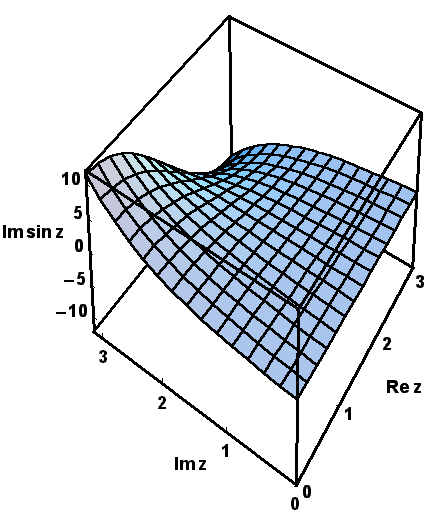
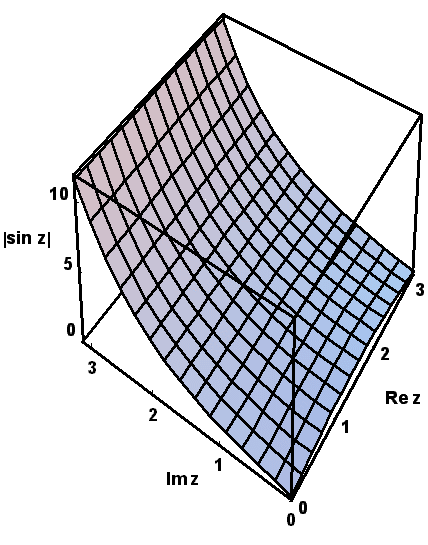
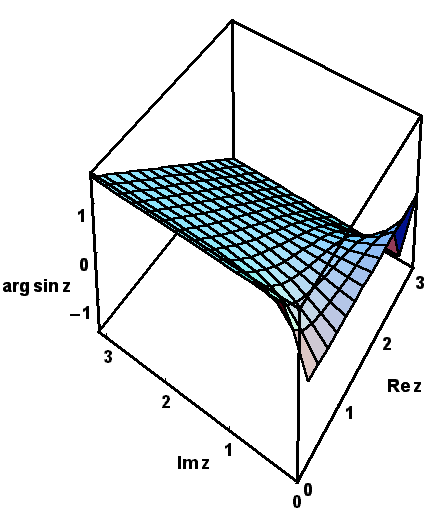
Plastischer als bei diesen zweidimensionalen Projektionen ist jedoch der Eindruck, den man erhält, wenn man die perspektivischen Darstellungen der Funktionswerte betrachtet, die die modernen Computer-Zeichenprogramme anbieten, wie in den nächsten Bildern gezeigt:
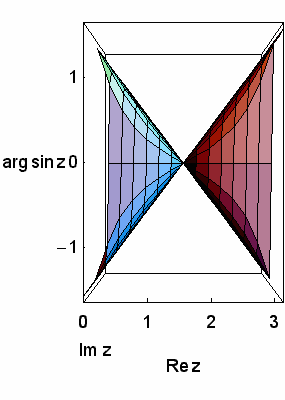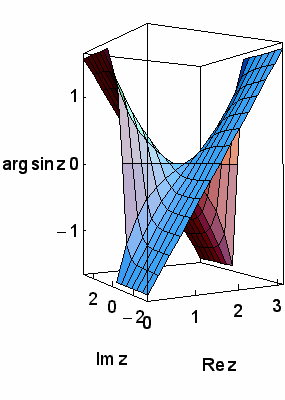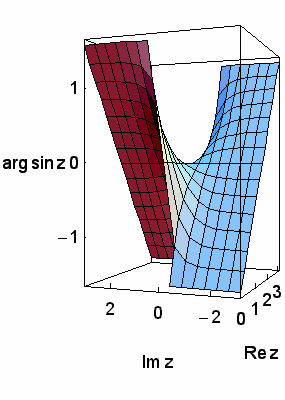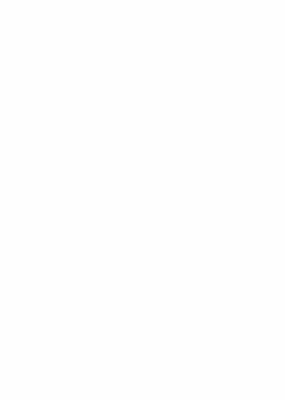
Um den Einfluß der Vorzeichenwechsel zu demonstrieren, haben wir Ihnen schließlich die vier interessierenden Variablen mit Hilfe des MATHEMATICA-Programms noch über dem größeren Rechteckgebiet 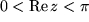 und
und 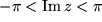 dargestellt, und zwar so dass sie sich drehen können:
dargestellt, und zwar so dass sie sich drehen können:
Nach Verschieben des Nullpunkts um 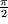 in Richtung der reellen Achse beschreiben diese Bilder das Gebirgsrelief der komplexen Cosinus-Funktion.
in Richtung der reellen Achse beschreiben diese Bilder das Gebirgsrelief der komplexen Cosinus-Funktion.
![]() ,
, ![]() und
und ![]() für allgemeine komplexe Variable
für allgemeine komplexe Variable ![]() :
:![]() erhält man daraus mit
erhält man daraus mit![]() und
und ![]() im Komplexen keineswegs mehr beschränkt sind, sondern für große Imaginärteile ansteigen wie die
Hyperbel-Funktionen.
im Komplexen keineswegs mehr beschränkt sind, sondern für große Imaginärteile ansteigen wie die
Hyperbel-Funktionen.![]() , z.B. der Fundamentalbereich mit
, z.B. der Fundamentalbereich mit ![]() , auf die zwischen
, auf die zwischen ![]() und
und ![]() aufgeschnittene zweiblättrige w-Ebene abgebildet.
aufgeschnittene zweiblättrige w-Ebene abgebildet.![]() über dem Quadrat
über dem Quadrat ![]() und
und ![]() zu betrachten:
zu betrachten:![]() , Imaginärteil
, Imaginärteil ![]() (gestrichelt), Betrag
(gestrichelt), Betrag ![]() und Argument
und Argument ![]() (ebenfalls gestrichelt) der Bildfunktion
(ebenfalls gestrichelt) der Bildfunktion ![]() über dem Quadrat.
über dem Quadrat.