Zum Abschluß dieses Kapitels schauen wir uns noch einige Umkehrfunktionen im Komplexen an, bei denen wieder charakteristische Unterschiede zum reellen Fall auftreten: als erstes betrachten wir die Wurzelfunktionen.
Nachdem wir gesehen haben, wie die n-te Potenz einen n-tel-Sektor der komplexen z-Ebene in die ganze w-Ebene abbildet, erwarten wir jetzt umgekehrt, dass die n-te Wurzel die ganze z-Ebene in einen n-tel-Sektor der w-Ebene abbildet, also eine n-wertige Funktion ist, wie wir sie ja im Komplexen bewußt zugelassen haben:
für
und
Wobei wir berücksichtigt haben, dass
ist.
Für das Argument
der unabhängigen Variablen
ist nach Vereinbarung
.
Für welche nichtnegativen ganzen Zahlen
gilt aber nun das Entsprechende für das Argument des Bildes ?
Demnach existieren genau n n-te Wurzeln
,
die wir mit dem Index
numerieren wollen:
für
.
Die komplexe Zahl
nennt man den Hauptwert. Wir sehen außerdem, dass die
Wurzeln auf einem Kreis mit dem Radius
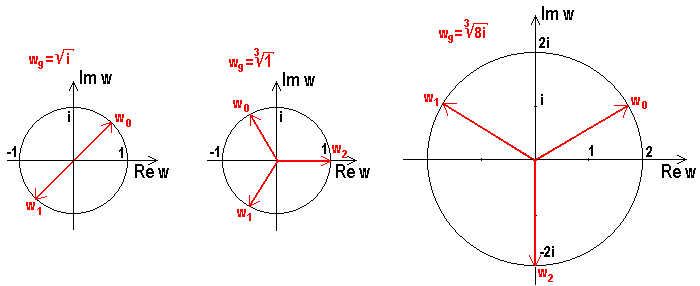
um den Ursprung auf den Ecken eines regelmäßigen n-Ecks liegen:
.
|
Aufgabe 8.12: Wurzeln Beweisen Sie
|
Als Beispiel berechnen wir zunächst
mit
und
, also
und
.
Ein weiteres Beispiel ist:
mit
, also
,
und
.
Als letzes Beispiel folgt:
mit
, also
,
und
.
,
b) 
und
c) 
.