Die Physiker legen Wert darauf, jede Stelle des Raum genau bezeichnen zu können, und verwenden dazu ein Koodinatensystem: Dazu wählen sie zunächst völlig willkürlich, aber oft sehr zweckmäßig einen Punkt des Raumes als Nullpunkt, auch Ursprung genannt. Durch diesen Punkt legen sie wieder völlig willkürlich drei beliebige reelle Zahlengeraden und numerieren sie: 
, 
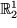und 
. Das ergibt bereits ein Koordinatensystem. Meist ist man jedoch etwas anspruchsvoller und verlangt, dass diese drei Geraden paarweise senkrecht aufeinander stehen: 
für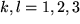 
. Das nennt man dann ein kartesisches Koordinatensystem. Wenn nun die positiven Halbgeraden der drei jetzt "Koordinatenachsen" genannten Zahlengeraden so angeordnet bzw. numeriert sind, dass die Drehung der positiven Halbgeraden der 1-Achse um den Winkel 
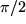um die 3-Achse in die positive Halbgerade der 2-Achse in Richtung der positiven 3-Achse gesehen eine Rechtsschraubendrehung darstellt (d.h. im Uhrzeigersinn erfolgt), dann hat man das Ideal, ein (kartesisches) Rechtskoordinatensystem konstruiert. Einigen von Ihnen ist diese Numerierung der Achsen auch als Rechte-Hand-Regel geläufig, weil die positiven Halbgeraden der 1-, 2- und 3-Achse dabei angeordnet sind wie Daumen, Zeigefinger und Mittelfinger der gespreizten rechten Hand. Im folgenden sei dies immer angenommen.
für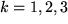 
liegt, jeweils wieder völlig willkürlich gewählt der zugehörige Einheitspunkt 
, dessen Entfernung vom Nullpunkt wie bei einem Lineal die Längeeinheit festlegt. So läßt sich jeder Punkt 
des dreidimensionalen Raums eindeutig durch ein Koordinatentripel reeller Zahlen kennzeichnen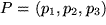 
. Die Zahl 
ist dabei jeweils die Höhe über der von den beiden anderen reellen Zahlengeraden 
und 
aufgespannten Koordinatenebene, gemessen in der vorher durch 